插入排序
插入排序 By Yujian
冒泡排序、选择排序、插入排序为基本的排序方法。
正如选择排序有直接选择和堆选择两种不同的方式,插入排序也有直接插入和希尔插入两种方式。
1直接插入排序:
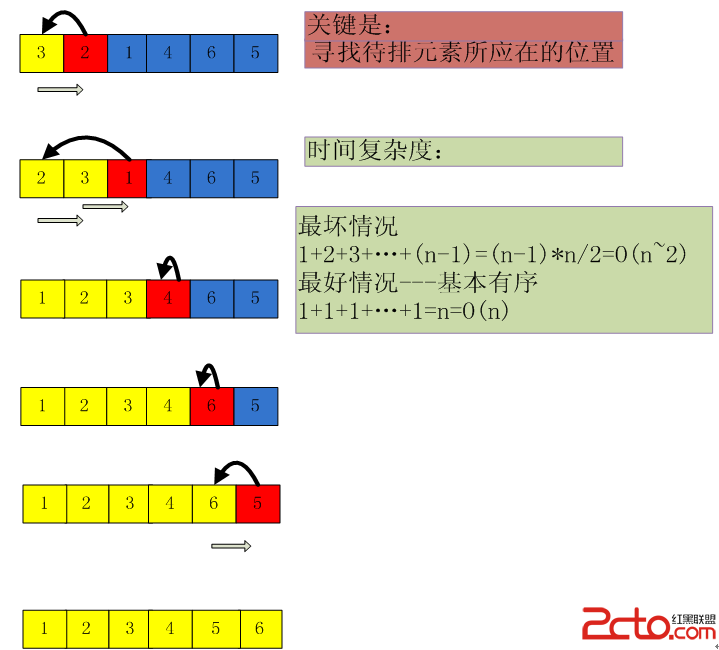
直接插入排序算法:
[cpp]
void InsertSort(int A[],int num)
{
int temp;
for (int i=1;i<num;i++) // i从开始,第i次循环时, 已排元素为,1,...,i-1 ; 待排元素为A[i]
{
temp=A[i]; // 保存待排元素
int j=i-1;
for (;j>=0;j--) // 已排元素逐个与待排元素比较 找到待排元素位置j+1
{
if (A[j]>temp)
{
A[j+1]=A[j];
}else
break;
}
A[j+1]=temp; // 找到位置后,将待排元素放入该位置
}
}
2 希尔插入排序
直接插入最坏情况下,时间复杂度为O(n~2),
而当基本有序时,排序的时间复杂度为O(n)
插入排序在对几乎已经排好序的数据操作时, 效率高, 可以达到线性排序的效率
但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
希尔排序是直接插入排序的改进算法,使用这种方法可以降低插入排序在最坏情况下的时间复杂度。
希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由1959年公布。
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。
区域的划分,不是将序列从某位置分开,左侧一组,右侧一组。而是采用步长分组的方法:相互间隔几个位置的元素为一组,间隔的长度称为步长。
这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序(冒泡排序或插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
原始的插入排序算法实现在最坏的情况下需要进行O(n2)的比较和交换。希尔排序的时间复杂度因步长串的不同而不同,目前已知的最好的步长串,可以使得希尔排序在最坏情况下的性能提升至O(n log2 n)。这比最好的比较算法的O(n log n)要差一些。
Shell 最初建议步长选择为n/2并且对步长取半直到步长达到1。虽然这样取可以比O(n2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。
可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如,如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。
希尔排序算法:
[cpp]
void ShellSort(int A[],int num)
{
int d=num/2;
int temp=0;
while (d>=1) // 步长
{
for (int i=0;i<d;i++) // 数组的起始位置
{
int j=i+d; // 待排元素的初始位置
while(j<num){
temp=A[j]; // 待排元素
int k=j-d; // 已排元素的最后位置
while(k>=0)
{
if (A[k]>temp)
{
A[k+d]=A[k];
}else
break;
k-=d;
}
A[k+d]=temp;
j+=d; // 下一个待排元素
}
}
d=d/2;
}
}
补充:软件开发 , C++ ,