C++ 拦截导弹问题
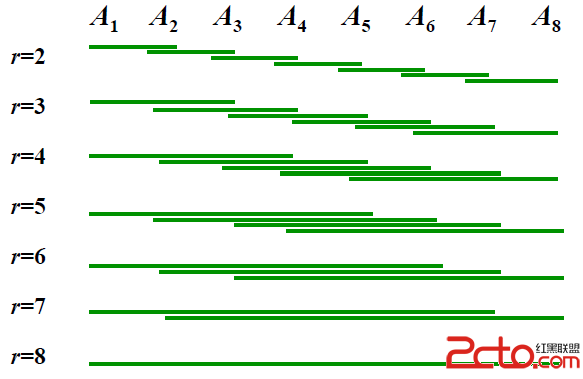
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入格式 Input Format
输入导弹依次飞来的高度(导弹数最多不超过20枚,雷达给出的高度数据是不大于30000的正整数)
输出格式 Output Format
计算这套系统最多能拦截多少导弹
如果要拦截所有导弹最少要配备多少套这种导弹拦截系统
样例输入
389 207 155 300 299 170 158 65
样例输出
6
2
追问:穷举是万金油 但是很多时候都不好用
这个题是用动态规划吧
答案:/*
已知当每套系统达到导弹拦截数最大,则所需要的系统数最少
在Choose函数中:
将导弹高度用一个数组(m_HList)存放,因为一套系统所能拦截的规律为,从左到右,依次递减
则,用一个栈(m_Stack)来存放所能拦截的导弹,并且用一个标志(NumAll)来记录一套系统的最
大拦截数目.用m_List来记录一套系统的拦截导弹号,然后当第二层循环结束时,代表一套系统
所能拦截的导弹已经最大.接下来用AllNumber来标志导弹是否被拦截完否则增加系统,以上同
理
*/
#include "iostream.h"
#define DATA int
#define MAX 5 // 导弹的数目
struct HighList
{
int Use; // 第几个系统拦截
DATA High; // 导弹的高度
};
class CStack{ // 堆栈类
public:
HighList m_aStack[MAX];
int m_iTop;
int Push(HighList Data) // 将数据压入栈中
{
if(m_iTop+1 > MAX)
return 0;
m_aStack[++m_iTop]=Data;
return 1;
}
DATA PopHigh(void) // 将栈中数据出栈
{
if(m_iTop == -1)
return -1;
return m_aStack[m_iTop--].High;
}
int MaxNumber(void) // 返回栈中数据个数
{
return m_iTop+1;
}
DATA Show(void) // 显示栈顶的数据
{
if(m_iTop == -1)
return -1;
return m_aStack[m_iTop].High;
}
CStack() // 初始化栈
{
int i;
for(i=0;i<MAX;i++)
{
m_aStack[i].High=0;
m_aStack[i].Use=0;
}
m_iTop=-1;
}
};
class CSystem{
protected:
CStack m_Stack;
HighList m_HList[MAX]; // 导弹的高度清单
void ListSign(int *p,int Num);
void SetObject(int *p,int MaxAll,int Object);
public:
int m_iMaxSystemNum; // 至少需要的拦截系统数
int m_iMaxNumber; // 一套系统最多可拦截的导弹数
CSystem(void)
{
m_iMaxSystemNum=0;
m_iMaxNumber=0;
}
void InputHigh(void) //输入高度
{
int i;
for(i=0;i<MAX;i++)
{
m_HList[i].Use=0;
cin>>m_HList[i].High;
}
}
void Choose();
void PrintHigh();
};
#include<iostream>
using namespace std;
int main(){
int h[21], opt[21], count, i, j, p[21], lis, pos, bul = 0, flis, flag;
count = 0;
while(cin>>h[count++]);
count--;
flag = count;
while(flag){
for(i = 0; i < count; i++){
opt[i] = 1;
p[i] = -1;
}
lis = 0;
for(i = count - 1; i >= 0; i--){
for(j = i + 1; j < count; j++){
if(h[i] != -1 && h[j] != -1 && h[i] >= h[j] && opt[j] + 1 > opt[i]){
opt[i] = opt[j] + 1;
p[i] = j;
}
}
if(opt[i] > lis){
lis = opt[i];
pos = i;
}
}
i = pos;
while(p[i] != -1){
h[i] = -1;
i = p[i];
flag--;
}
h[i] = -1;
flag--;
if(!bul){
flis = lis;
}
bul++;
}
printf("%d\n%d\n", flis, bul);
}
第一个问题用递归算法,穷举所有递减数列,找出最长的递减数列,总是容易解决的。
第二个问题似乎很难穷举所有的递减数列集合,找出集合元素最少的集合。
这道题是最长非下降子序列问题,一般考虑用递归 / 动态规划求解。当然,如果数据规模不大,可以考虑穷举。
为了防御敌国的导弹袭击,发展出一种导弹拦截系统
上一个:用C++写程序
下一个:C++程序设计 题目