Codeforces Round #178 (Div. 2)

C题：

蛮有意思的，给你m个位置，现在要从这m个位置往位置的两边扩展，问你把所有的数都扩展到总共有多少种方法。

在两个位置中间的那些数的可能的排列数应该是2^（k-1），因为每次都有两种选择，要么左端点，要么右端点。

然后从所有的间隔中各取出一种排列，a1 a2 a3 b1 b2 b3 c1 c2 c3，现在就是求这个序列的总排列数，要求同类的先后顺序不能变，很容易发现这个其实就是类似于多重集合的排列，ans=n!/(p1!*p2!*p3!) ，然后分子再乘上一个2^(k-1)就好了

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long lld;
const int inf = ~0u>>2;
const int mod = 1000000007 ;
const int maxn = 1010;
int pos[maxn];
lld Pow(lld a,lld b) {
    lld ans = 1;
    while(b) {
        if(b&1) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans ;
}
lld fac[maxn],two[maxn];
vector<int> rec;
void solve(int n) {
     fac[0] = 1; two[0] = 1;
     for(int i = 1; i <= 1000; i++) fac[i] = fac[i-1] * i % mod;
     for(int i = 1; i <= 1000; i++) two[i] = two[i-1] * 2 % mod;
     int sum = 0;
     for(int i = 0; i < rec.size(); i++) sum += rec[i];
    // printf("sum=%d\n",sum);
     lld ans = fac[sum];
     for(int i = 0; i < rec.size(); i++) {
         ans = ans * Pow(fac[rec[i]],mod-2) % mod;
     }
     for(int i = 1; i < rec.size()-1;i++) {
      if(rec[i]>0) ans = ans * two[rec[i]-1] % mod;
     //   printf("ans=%d\n",rec[i]);
     }
     printf("%I64d\n",ans);
}

int main() {
    int n , m;
    scanf("%d%d",&n,&m);
    for(int i = 0; i < m; i++) {
        scanf("%d",&pos[i]);
    }
    sort(pos,pos+m);
    rec.push_back(pos[0]-1);
    for(int i = 1; i < m ; i++) {
       rec.push_back(pos[i]-pos[i-1]-1);
    }
    rec.push_back(n-pos[m-1]);
    solve(n);
    return 0;
}

D题：

上次做过一个网格反弹的题，，，，被陷进去了。。。。

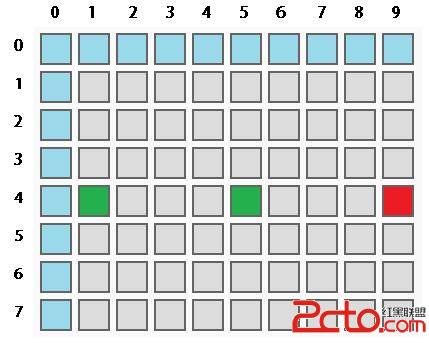
网格中的反弹有个性质就是45度反射的时候经过的格子的奇偶性都是一样的，所以无论怎么反弹，都不会经过两个相邻的方格。

给你一个n*m的矩形网格，问你从某个位置，某个方向出发经过多少个格子才能将网格染成棋盘的样子，也就是每两个相邻的格子的颜色都不同。

每个矩形有两种棋盘，不管哪种，如果成功染成某一种，肯定会经过边界的网格n+m-2次，也就是说，如果反弹过程中经过了n+m-2个不同的边界网格，肯定就对应着一种棋盘的方案，如果两次到达同一个位置同一个方向，肯定已经进入循环了。

E题：

给你一棵树，5000个点，每条边有边权，可以删掉一条边再将这条边换个位置，要保证改变后仍然是树的形状，现在问你所有点对的距离之和最小是多少。

5000个点，马上想到n^2..然后就是暴力枚举去掉每条边，剩下的就是两棵树，然后重新连接一条边，稍微想一下，这条边肯定就是将两棵树的重心连起来，所以，接下来的事情就简单了。。。

比赛的时候看错了题，以为边可以修改很多次。。。然后各种YY，不够仔细啊。。。

--------------------------------------------------------------------------------

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int inf = ~0u>>2;
const int mod = 1000000007 ;
const int maxn = 5010;
int son[maxn] ;
long long dp[maxn];
int n ;
int mp[maxn][maxn];
vector<int> edge[maxn];
int node;
struct Edge{
    int s,t,w;
    Edge(){}
    Edge(int a,int b,int c)
    {
        s = a;
        t = b;
        w = c;
    }
}in[maxn];
int dep[maxn];
void dfs(int u,int f) {
    son[u] = 1;
    dep[u] = dep[f] + 1;
    int sz = edge[u].size();
    for(int i = 0; i < sz; i++) {
        int v = edge[u][i];
        if(v==f) continue;
        dfs(v,u);
        son[u] += son[v];
    }
}
int cen;
int S[maxn];
void DFS(int u,int f) {
    S[u] = 1;
    int sz = edge[u].size();
    for(int i = 0; i < sz; i++) {
        int v = edge[u][i];
        if(v == f || v == node) continue;
        DFS(v,u);
        S[u] += S[v];
    }
}
long long sum;
void dfs1(int u,int f,int rt) {
     dp[u] = 0;
     int sz = edge[u].size();
     for(int i = 0; i < sz; i++) {
        int v = edge[u][i];
        if(v == f || v == node) continue;
        dfs1(v,u,rt);
        sum += (long long ) S[v] * (S[rt]-S[v]) * mp[u][v];
        dp[u] += dp[v] + (long long)S[v] * mp[u][v];
     }
}
long long Mi;
void dfs2(int u,int f,int rt) {
    if(u==rt) {
        Mi = min(dp[u],Mi);
    } else {
        long long tmp = dp[f] - dp[u] - (long long)S[u] * mp[f][u];
        dp[u] += (long long)mp[f][u] * (S[rt] - S[u]) + tmp;
        Mi = min(dp[u],Mi);
    }
    int sz = edge[u].size();
    for(int i = 0; i < sz; i++) {
        int v = edge[u][i];
        if(v == f || v == node) continue;
        dfs2(v,u,rt) ;
    }
}
int main() {
    scanf("%d",&n);
    int a,b,c;
    int tot = 0;
    for(int i=1;i<n;i++) {
        scanf("%d%d%d",&a,&b,&c);
        edge[a].push_back(b);
        edge[b].push_back(a);
        mp[a][b] = mp[b][a] = c;
  &nbs

补充：软件开发 , C++ ,