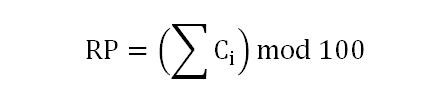HDU4635(Strongly connected)Tarjan算法,强连通+缩点

 
/* 
 *题目大意： 
 *给你一个DAG图,问你最多能添加多少条边使得这个DAG图依然不是强联通的; 
 * 
 *算法思想： 
 *强连通+缩点 
 *最终添加完边的图,肯定可以分成两个部X和Y,其中只有X到Y的边没有Y到X的边; 
 *那么要使得边数尽可能的多,则X部肯定是一个完全图,Y部也是,同时X部中每个点到Y部的每个点都有一条边; 
 *假设X部有x个点,Y部有y个点,则x+y=n; 
 *同时边数F=x*y+x*(x-1)+y*(y-1),然后去掉已经有了的边m,则为答案; 
 *当x+y为定值时,二者越接近,x*y越大，所以要使得边数最多,那么X部和Y部的点数的个数差距就要越大; 
 *对于给定的有向图缩点,对于缩点后的每个点,如果它的出度或者入度为0,那么它才有可能成为X部或者Y部; 
 *然后找出最大值即可; 
**/  
#include<iostream>  
#include<cstdio>  
#include<cstring>  
#include<algorithm>  
using namespace std;  
  
const int N=200010;  
const int M=400010;  
const int INF=0xffffffff;  
  
typedef long long LL;  
  
struct Edge  
{  
    int to,next;  
} edge[M];  
  
LL n,m,cnt,head[N];  
LL dep,top,atype;  
  
LL dfn[N],low[N],vis[N],stack[N],belong[N],in[N],out[N],sum[N];  
  
void addedge(int u,int v)  
{  
    edge[cnt].to=v;  
    edge[cnt].next=head[u];  
    head[u]=cnt++;  
}  
  
void Tarjan(int u)  
{  
    dfn[u]=low[u]=++dep;  
    stack[top++]=u;  
    vis[u]=1;  
    for(int i=head[u]; i!=-1; i=edge[i].next)  
    {  
        int v=edge[i].to;  
        if(!dfn[v])  
        {  
            Tarjan(v);  
            low[u]=min(low[u],low[v]);  
        }  
        else if(vis[v])  
        {  
            low[u]=min(low[u],dfn[v]);  
        }  
    }  
    int j;  
    if(dfn[u]==low[u])  
    {  
        atype++;  
        do  
        {  
            j=stack[--top];  
            belong[j]=atype;  
            sum[atype]++;   //记录每个连通分量中点的个数  
            vis[j]=0;  
        }  
        while(u!=j);  
    }  
}  
  
void solve()  
{  
    if(n==1)  
    {  
        puts("-1");  
        return;  
    }  
    cnt=dep=top=atype=0;  
    memset(head,-1,sizeof(head));  
    memset(dfn,0,sizeof(dfn));  
    memset(low,0,sizeof(low));  
    memset(vis,0,sizeof(vis));  
    memset(belong,0,sizeof(belong));  
    memset(in,0,sizeof(in));  
    memset(out,0,sizeof(out));  
    memset(sum,0,sizeof(sum));  
  
    int u,v;  
    for(int i=0; i<m; i++)  
    {  
        scanf("%d%d",&u,&v);  
        addedge(u,v);  
    }  
  
    for(int i=1; i<=n; i++)  
        if(!dfn[i])  
            Tarjan(i);  
    if(atype==1)  
    {  
        puts("-1");  
        return;  
    }  
    for(int u=1; u<=n; u++)  
        for(int i=head[u]; i!=-1; i=edge[i].next)  
        {  
            int v=edge[i].to;  
            if(belong[u]!=belong[v])  
            {  
                out[belong[u]]++;  
                in[belong[v]]++;  
            }  
        }  
    LL ans=0,tmp;  
    for(int i=1; i<=atype; i++)  
        if(in[i]==0 || out[i]==0)     //找出度或者入度为0的点，包含节点数最少的那个点  
        {  
            tmp=sum[i];//令它为一个部，其它所有点加起来做另一个部，就可以得到最多边数的图了  
            ans=max(ans,tmp*(tmp-1)+(n-tmp)*(n-tmp-1)+tmp*(n-tmp)-m);  
        }  
    printf("%d\n",ans);  
}  
  
int main()  
{  
  
    //freopen("C:\\Users\\Administrator\\Desktop\\kd.txt","r",stdin);  
    int t1,t2=0;  
    scanf("%d",&t1);  
    while(t1--)  
    {  
        t2++;  
        printf("Case %d: ",t2);  
        scanf("%d%d",&n,&m);  
        solve();  
    }  
    return 0;  
}

补充：软件开发 , C++ ,