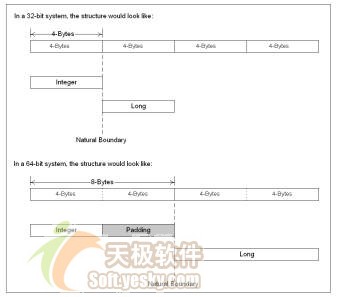
UFLDL练习(PCA and Whitening && Softmax Regression)
softmax纠结了两天,原因是自己不小心改了主程序还是照例只是贴贴代码,如果你有需要的话可以去看UFLDL的教程
至于效果和UFLDL都是一样的,我就不重复贴图了啊,ps:代码是matlab的,不是python的
PCA and Whitening:
pca_gen.m
[python]
%%================================================================
x = sampleIMAGESRAW();
figure('name','Raw images');
randsel = randi(size(x,2),200,1); % A random selection of samples for visualization
display_network(x(:,randsel));
%%================================================================
avg = mean(x,2);
x = x - repmat(avg,1,size(x,2));
%%================================================================
xRot = zeros(size(x)); % You need to compute this
[u,s,v]=svd(x);
xRot = u'*x;
%%================================================================
covar = zeros(size(x, 1)); % You need to compute this
covar = diag(diag(cov(x')));
%%================================================================
figure('name','Visualisation of covariance matrix');
imagesc(covar);
%%================================================================
k = 0; % Set k accordingly
egis=eig(covar)
egis=sort(egis,'descend')
for i=1:size(covar,1)
if (sum(egis(1:i))/sum(egis)>0.99)
k=i
break;
end
end
%%================================================================
%%================================================================
xHat = zeros(size(x)); % You need to compute this
xHat = u*[xRot(1:k,:);zeros(size(xHat(k+1:end,:)))];
% Visualise the data, and compare it to the raw data
% You should observe that the raw and processed data are of comparable quality.
% For comparison, you may wish to generate a PCA reduced image which
% retains only 90% of the variance.
figure('name',['PCA processed images ',sprintf('(%d / %d dimensions)', k, size(x, 1)),'']);
display_network(xHat(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));
%%================================================================
%% Step 4a: Implement PCA with whitening and regularisation
% Implement PCA with whitening and regularisation to produce the matrix
% xPCAWhite.
epsilon = 0.1;
xPCAWhite = zeros(size(x));
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch.
x = x - repmat(avg, size(x, 1), 1);
sigma = x * x' / size(x, 2);
[U,S,V] = svd(sigma);
xRot = U' * x; % rotated version of the data.
xTilde = U(:,1:k)' * x; % reduced dimension representation of the data,
% where k is the number of eigenvectors to keep
xPCAWhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;
%%================================================================
% Visualise the covariance matrix. You should see a red line across the
% diagonal against a blue background.
covar = diag(diag(cov(xPCAWhite')));
figure('name','Visualisation of covariance matrix');
imagesc(covar);
%%================================================================
xZCAWhite = zeros(size(x));
xZCAWhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;
%%================================================================
figure('name','ZCA whitened images');
display_network(xZCAWhite(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));
Softmax Regression
softmaxCost.m
[python]
function [cost, grad] = softmaxCost(theta, numClasses, inputSize, lambda, data, labels)
% numClasses - the number of classes
% inputSize - the size N of the input vector
% lambda - weight decay parameter
% data - the N x M input matrix, where each column data(:, i) corresponds to
% a single test set
% labels - an M x 1 matrix containing the labels corresponding for the input data
%
% Unroll the parameters from theta
theta = reshape(theta, numClasses, inputSize);
numCases = size(data, 2);
groundTruth = full(sparse(labels, 1:numCases, 1)); %numClasses*M
cost = 0;
thetagrad = zeros(numClasses, inputSize);
M = theta*data; % (numClasses,N)*(N,M)
M = bsxfun(@minus, M, max(M, [], 1));
h = exp(M);
h = bsxfun(@rdivide, h, sum(h));
cost = -1/numCases*sum(sum(groundTruth.*log(h)))+lambda/2*sum(sum(theta.^2));
thetagrad = -1/numCases*((groundTruth-h)*data')+lambda*theta;%log(h)
下面一段是关键部分没有Vectorization版本的代码
%for i=1:numCases
% s=groundTruth(:,i).*log(h(:,i));
% cost=cost+sum(s);
%end
%cost=cost*(-1)/numCases+lambda/2*sum(sum(theta.^2));
%for i=1:numClasses
% for j=1:numCases
% %groundTruth(:,j)
% %h(:,j)
% k=((groundTruth(:,j)-h(:,j))*data(:,j)');
%
% thetagrad(i,:)=thetagrad(i,:)+k(i,:);
% end
% thetagrad(i,:)=-thetagrad(i,:)/numCases+lambda*theta(i,:);
%end
grad = [thetagrad(:)];
end
补充:Web开发 , Python ,