数据结构：线段树

一、线段树基本概念
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

性质：父亲的区间是[a,b],(c=(a+b)/2)左儿子的区间是[a,c]，右儿子的区间是[c+1,b]，线段树需要的空间为数组大小的四倍

二、线段树的存储数据结构
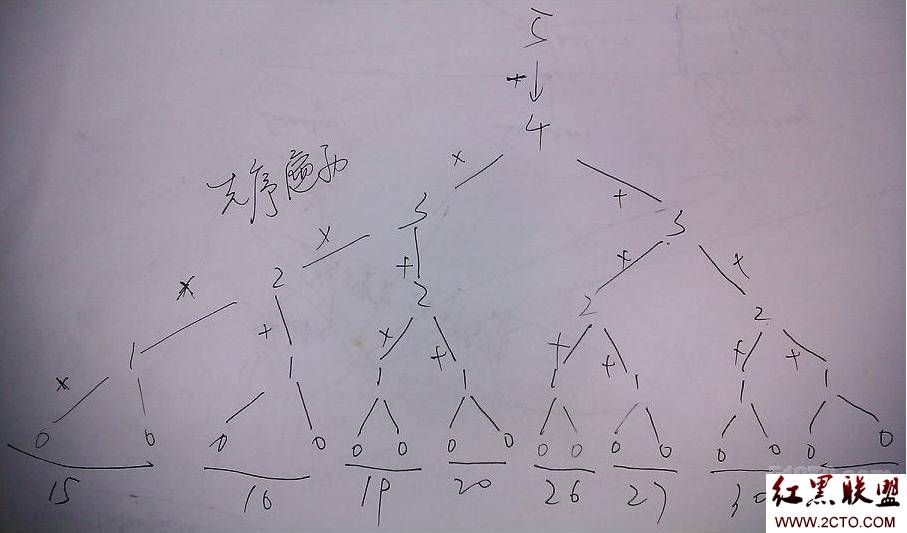
由上面的图可以看出，存储一颗线段树和二叉树有点类似，需要左孩子和右孩子节点，另外，为了存储每条线段出现的次数，所以一般会加上计数的元素，其具体如下：

[cpp]
struct Node         // 线段树
{
    int left;
    int right;
    int counter;
}segTree[4*BORDER];

struct Node // 线段树
{
int left;
int right;
int counter;
}segTree[4*BORDER];
其中，;left代表左端点、right代表右端点，counter代表每条线段出现的次数，BORDE代表线段端点坐标不超过100。由上面的性质可以知道，我们需要4倍的空间来存储。

三、线段树支持的操作
一颗线段树至少支持以下四个操作：

void construct(int index, int lef, int rig)，构建线段树根节点开始构建区间[lef,rig]的线段树
void insert(int index, int start, int end)，插入线段[start,end]到线段树, 同时计数区间次数
int query(int index, int x)，查询点x的出现次数，从根节点开始到[x,x]叶子的这条路径中所有点计数相加方为x出现次数
void delete_ (int c , int d, int index)，从线段树中删除线段[c,d]

具体操作如下：

1、线段树的创建

[cpp]
/* 构建线段树根节点开始构建区间[lef,rig]的线段树*/
void construct(int index, int lef, int rig)
{
    segTree[index].left = lef;
    segTree[index].right = rig;
    if(lef == rig)   // 叶节点
    {
        segTree[index].counter = 0;
        return;
    }
    int mid = (lef+rig) >> 1;
    construct((index<<1)+1, lef, mid);
    construct((index<<1)+2, mid+1, rig);
    segTree[index].counter = 0;
}

/* 构建线段树根节点开始构建区间[lef,rig]的线段树*/
void construct(int index, int lef, int rig)
{
segTree[index].left = lef;
segTree[index].right = rig;
if(lef == rig)   // 叶节点
{
  segTree[index].counter = 0;
  return;
}
int mid = (lef+rig) >> 1;
construct((index<<1)+1, lef, mid);
construct((index<<1)+2, mid+1, rig);
segTree[index].counter = 0;
}

2、线段树的元素插入

[cpp]
/* 插入线段[start,end]到线段树, 同时计数区间次数 */
void insert(int index, int start, int end)
{
    if(segTree[index].left == start && segTree[index].right == end)
    {
        ++segTree[index].counter;
        return;
    }
    int mid = (segTree[index].left + segTree[index].right) >> 1;
    if(end <= mid)//左子树
    {
        insert((index<<1)+1, start, end);
    }else if(start > mid)//右子树
    {
        insert((index<<1)+2, start, end);
    }else//分开来了
    {
        insert((index<<1)+1, start, mid);
        insert((index<<1)+2, mid+1, end);
    }
}

/* 插入线段[start,end]到线段树, 同时计数区间次数 */
void insert(int index, int start, int end)
{
if(segTree[index].left == start && segTree[index].right == end)
{
  ++segTree[index].counter;
  return;
}
int mid = (segTree[index].left + segTree[index].right) >> 1;
if(end <= mid)//左子树
{
  insert((index<<1)+1, start, end);
}else if(start > mid)//右子树
{
  insert((index<<1)+2, start, end);
}else//分开来了
{
  insert((index<<1)+1, start, mid);
  insert((index<<1)+2, mid+1, end);
}
}
3、线段树的元素查找

[cpp]
/* 查询点x的出现次数
* 从根节点开始到[x,x]叶子的这条路径中所有点计数相加方为x出现次数
*/
int query(int index, int x)
{
    if(segTree[index].left == segTree[index].right) // 走到叶子，返回
    {
        return segTree[index].counter;
    }
    int mid = (segTree[index].left+segTree[index].right) >> 1;
    if(x <= mid)
    {
        return segTree[index].counter + query((index<<1)+1,x);
    }
    return segTree[index].counter + query((index<<1)+2,x);
}

/* 查询点x的出现次数
* 从根节点开始到[x,x]叶子的这条路径中所有点计数相加方为x出现次数
*/
int query(int index, int x)
{
if(segTree[index].left == segTree[index].right) // 走到叶子，返回
{
  return segTree[index].counter;
}
int mid = (segTree[index].left+segTree[index].right) >> 1;
if(x <= mid)
{
  return segTree[index].counter + query((index<<1)+1,x);
}
return segTree[index].counter + query((index<<1)+2,x);
}4、线段树的元素删除
[cpp]
void delete_ (int c , int d, int index)
{
       if(c <= segTree[index].left && d >= segTree[index].right)
           segTree[index].counter--;
       else
       {
          if(c < (segTree[index].left + segTree[index].right)/2 ) delete_( c,d, segTree[index].left);
          if(d > (segTree[index].left + segTree[index].right)/2 ) delete_( c,d, segTree[index].right);
       }
}

void&n

补充：软件开发 , C++ ,