用js检测两个线段是否相交
在图形编程中,经常需要检测两个线段是否相交,例如,不规则图形的碰撞检测,检测线段的碰撞时基础.
线段不是直线,计算起来会麻烦一点,而且有很多种方法,这里就介绍一种向量法的解法.
如何检测两条线段是相交的呢?首先需要四个点p1,p2,p3,p4,其中p1和p2表示一条线段,p3和p4表示第二条线段.
然后,推导,如果两条线段相交,那么对于第一条线段来说(由p1和p2为端点)p3和p4必然是分别在它两边的.同时,对于第二条线段来说(由p3和p4为端点),p1和p2也必然是在第二条线段的两边的.反过来,要证明两条线段相交,只需要证明后面的两个条件即可,这是一个充分必要条件.
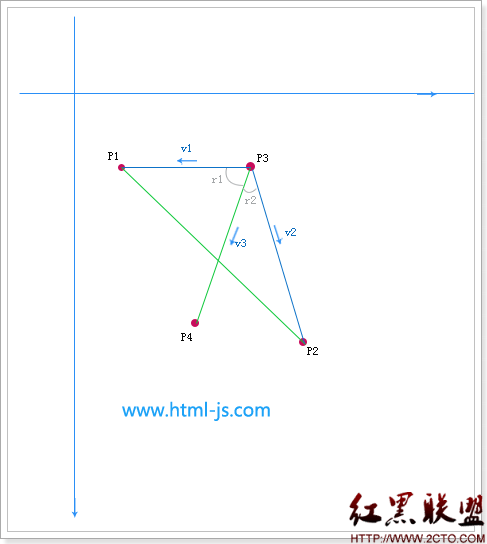
那么如何证明两个点分别在一条直线的两边呢?用向量法,看图:
图中,p1,p2,p3,p4对应四个点,表示两条绿色的线段,我们先用线段p3->p4为基准线,判断p1和p2是否在它的两边.
如图,根据四个点,建立三个向量,v1,v2,v3,方向在图中已经标示清楚.
要判断p1和p2是否在线段的两侧,需要先计算v1×v3和v2×v3的值,这里涉及到向量的乘法,这里用到的是叉乘,
向量a和向量b叉乘得出来的结果是一个和向量a,向量b组成的平面垂直方向的一个向量,它的值有正负之分.
这里,我们利用叉乘得出来的结果来指导夹角的方向, v1×v3和v2×v3两个结果如果是同号的,就说明,两个点在线段的同一侧,如果是异号的,说明,两个点在线段的不同侧.
最后,其实我们就是判断下( v1×v3)*(v2×v3)<=0 说明他们在不同侧.
向量的叉乘公式是: V1(x1, y1) ×V2(x2, y2) = x1y2 –y1x2
然后,接着,用同样的方式判断一下以p1->p2作为基准线,判断p3和p4是否在两边,如果都满足了,那说明两个线段是相交的.
js实现如下:
01
//计算叉乘
02
var crossMul=function(v1,v2){
03
return v1.x*v2.y-v1.y*v2.x;
04
}
05
//相交返回true
06
var checkCross=function(p1,p2,p3,p4){
07
var v1={x:p1.x-p3.x,y:p1.y-p3.y},
08
v2={x:p2.x-p3.x,y:p2.y-p3.y},
09
v3={x:p4.x-p3.x,y:p4.y-p3.y},
10
v=crossMul(v1,v3)*crossMul(v2,v3)
11
v1={x:p3.x-p1.x,y:p3.y-p1.y}
12
v2={x:p4.x-p1.x,y:p4.y-p1.y}
13
v3={x:p2.x-p1.x,y:p2.y-p1.y}
14
return (v<=0&&crossMul(v1,v3)*crossMul(v2,v3)<=0)?true:false
15
}
然后这样调用:
01
checkCross({
02
x:0,
03
y:0
04
},{
05
x:100,
06
y:100
07
},{
08
x:20,
09
y:0
10
},{
11
x:50,
12
y:40
13
})
这里有个简单的demo,不过参数是写死的....没空写了....
http://www.html-js.com/mj/version1.0.3/lab/point-rect-test.html
补充:web前端 , JavaScript ,