CF 260E Dividing Kingdom(枚举+线段树)

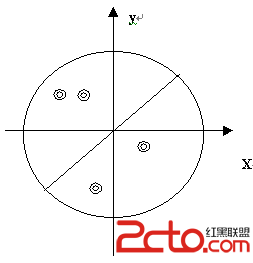
题目：给出一些点，要求给出4条线，两条平行x轴，两条平等y轴，不经过任何点，把平面分为9块，每块包含的点数，正数可以满足每个人的需要

当给定每一个方块的人数之后，我们便可以求出4条线的坐标

这个我们按x,y坐标排序，取前多少个就行了。

但是这样只是在宏观上大致求出坐标，还需要考察若干个分块，查询数量，进行比较

那么关于查询每个分块的数量的话，我是通过线段树实现的

而且比较暴力

根据x坐标建立线段树，每个结点存放了一个vector，表示这个区间内所有的点的y坐标值

查询的时候，直接二分vector就行了

[cpp]

#include<iostream>

#include<cstdio>

#include<map>

#include<cstring>

#include<cmath>

#include<vector>

#include<algorithm>

#include<set>

#include<string>

#include<queue>

#define inf 1000000005

#define M 40

#define N 100005

#define maxn 300005

#define eps 1e-12

#define zero(a) fabs(a)<eps

#define Min(a,b) ((a)<(b)?(a):(b))

#define Max(a,b) ((a)>(b)?(a):(b))

#define pb(a) push_back(a)

#define mp(a,b) make_pair(a,b)

#define mem(a,b) memset(a,b,sizeof(a))

#define LL long long

#define MOD 1000000007

#define lson step<<1

#define rson step<<1|1

#define sqr(a) ((a)*(a))

#define Key_value ch[ch[root][1]][0]

#define test puts("OK");

#define pi acos(-1.0)

#define lowbit(x) ((-(x))&(x))

#define HASH1 1331

#define HASH2 10001

#pragma comment(linker, "/STACK:1024000000,1024000000")

using namespace std;

struct Set_tree{

int left,right;

vector<int>v;

}L[N*4];

struct Point{

int x,y;

bool operator<(const Point n)const{

return x!=n.x?x<n.x:y<n.y;

}

}p[N];

int n,x[N],y[N];

int a[9],b[9];

double ret_x1,ret_x2,ret_y1,ret_y2;

void Bulid(int step,int l,int r){

L[step].left=l;

L[step].right=r;

L[step].v.clear();

for(int i=l;i<=r;i++)

L[step].v.pb(p[i].y);

sort(L[step].v.begin(),L[step].v.end());

if(l==r)

return;

int m=(l+r)>>1;

Bulid(lson,l,m);

Bulid(rson,m+1,r);

}

int Query(int step,int l,int r,int val){

if(L[step].left==l&&r==L[step].right){

if(L[step].v.size()==0) return 0;

if(L[step].v[0]>val) return 0;

if(L[step].v.back()<=val) return L[step].v.size();

return (upper_bound(L[step].v.begin(),L[step].v.end(),val)-L[step].v.begin());

}

int m=(L[step].left+L[step].right)>>1;

if(r<=m) return Query(lson,l,r,val);

else if(l>m) return Query(rson,l,r,val);

else return Query(lson,l,m,val)+Query(rson,m+1,r,val);

}

bool ok(){

int x1=b[a[0]]+b[a[1]]+b[a[2]]-1;

int x2=x1+b[a[3]]+b[a[4]]+b[a[5]];

int y1=b[a[0]]+b[a[3]]+b[a[6]]-1;

int y2=y1+b[a[1]]+b[a[4]]+b[a[7]];

if(x1+1>=n||x[x1]==x[x1+1]) return false;

if(x2+1>=n||x[x2]==x[x2+1]) return false;

if(y1+1>=n||y[y1]==y[y1+1]) return false;

if(y2+1>=n||y[y2]==y[y2+1]) return false;

if(Query(1,0,x1,y[y1])!=b[a[0]]) return false;

if(Query(1,0,x1,y[y2])!=b[a[0]]+b[a[1]]) return false;

if(Query(1,x1+1,x2,y[y1])!=b[a[3]]) return false;

if(Query(1,x1+1,x2,y[y2])!=b[a[3]]+b[a[4]]) return false;

ret_x1=(x[x1]+x[x1+1])/2.0;

ret_x2=(x[x2]+x[x2+1])/2.0;

ret_y1=(y[y1]+y[y1+1])/2.0;

ret_y2=(y[y2]+y[y2+1])/2.0;

return true;

}

int main(){

//freopen("input.txt","r",stdin);

while(scanf("%d",&n)!=EOF){

for(int i=0;i<n;i++){

scanf("%d%d",&p[i].x,&p[i].y);

x[i]=p[i].x;y[i]=p[i].y;

}

sort(p,p+n);

sort(x,x+n);

sort(y,y+n);

Bulid(1,0,n-1);

for(int i=0;i<9;i++) scanf("%d",&b[i]);

for(int i=0;i<9;i++) a[i]=i;

int t=362880;

while(t--){

if(ok()){

printf("%.1f %.1f\n%.1f %.1f\n",ret_x1,ret_x2,ret_y1,ret_y2);

break;

}

next_permutation(a,a+9);

}

if(t<=0) puts("-1");

}

return 0;

}