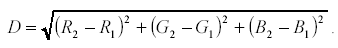hdu3694 Fermat Point in Quadrangle 费马点

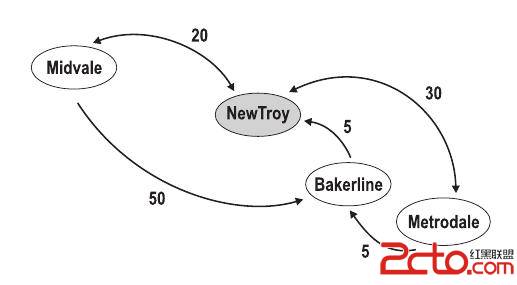
题意：给出四个点构成四边形（不按顺序给），求费马距离。

1.因为只有四个点，当这四个点可以构成凸四边形时（如图）：对角线形成的交点是费马点。就是点1，根据三角形的两边大于第三边可证明。

2.当不能构成凸多边形时，就是那个凹点是费马点（如图）：同理可证。

代码如下：//有点难看 TT
[cpp]
#include<cstdio>
#include<iostream>
#include<math.h>
#define eps 1e-8
using namespace std;

const int maxn=4;
struct point{double x,y;}points[maxn];
int n=4;

double dis(point p1,point p2)
{
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
double alldis(point tmp)
{
    double sum=0;
    int i;
    for(i=0;i<n;i++)
    {
        sum+=dis(tmp,points[i]);
    }
    return sum;
}

double xmult(point p1,point p2,point p0)
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
point intersection(point p1,point p2,point p3,point p4)
{
    point ret=p1;
    double t=((p1.x-p3.x)*(p3.y-p4.y)-(p1.y-p3.y)*(p3.x-p4.x))
        /((p1.x-p2.x)*(p3.y-p4.y)-(p1.y-p2.y)*(p3.x-p4.x));
    ret.x+=(p2.x-p1.x)*t;
    ret.y+=(p2.y-p1.y)*t;
    return ret;
}

double min(double a,double b)
{
    return a>b? b:a;
}
int main()
{
    while(1)
    {
        int i;
        for(i=0;i<4;i++)
            scanf("%lf%lf",&points[i].x,&points[i].y);
        if(points[0].x==-1&&points[1].x==-1&&points[2].x==-1&&points[3].x==-1&&
            points[0].y==-1&&points[1].y==-1&&points[2].y==-1&&points[3].y==-1)break;

        double res=0;
        double minn=1000000000;
        for(i=0;i<n;i++)
        {
            res=alldis(points[i]);
            minn=min(minn,res);
        }
        if(xmult(points[0],points[1],points[3])*xmult(points[2],points[1],points[3])<0)
        {
            point ans=intersection(points[0],points[2],points[1],points[3]);
            res=alldis(ans);
            minn=min(minn,res);

        }
        if(xmult(points[1],points[2],points[3])*xmult(points[0],points[2],points[3])<0)
        {
            point ans=intersection(points[1],points[0],points[2],points[3]);
            res=alldis(ans);
            minn=min(minn,res);
        }
        if(xmult(points[2],points[0],points[3])*xmult(points[1],points[0],points[3])<0)
        {
            point ans=intersection(points[2],points[1],points[0],points[3]);
            res=alldis(ans); www.zzzyk.com
            minn=min(minn,res);
        }
        printf("%.4lf\n",minn);
    }
    return 0;
}
作者：ssslpk

补充：软件开发 , C++ ,