POJ 1631(O(nlogn)LIS的2种做法)

Bridging signals
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 8574 Accepted: 4635
Description
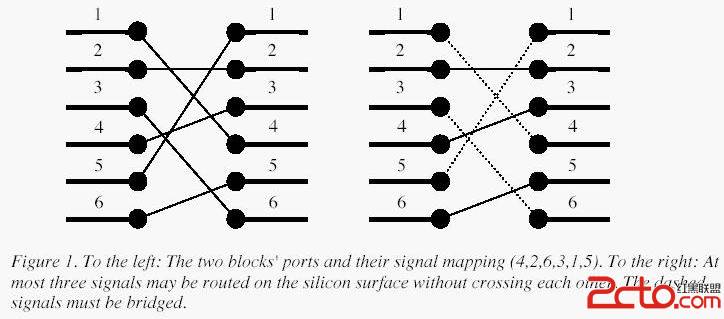
对于一个二分图的完全匹配，请找出最多的边使其两两不相交。

Input
第一行为测试数据数t，
对于每组数据，第一行为匹配数 p < 40000，
接下来p行，每行1个数a[i]，表示左边第i个端点与右边第a[i]个端点相连
Output
对每组数据，输出一行ans，表示最大不相交匹配数
Sample Input
4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6
Sample Output
3
9
1
4
Source
Northwestern Europe 2003
这题显然可以转化为a[i]的LIS
LIS的一般做法如下：
f[i]表示以i为最后一个元素的最长序列数，
f[i]=f[j]+1(a[j]<a[i]，j<i)
nLogn 算法1：
显然上面的方程有1维n是用来求‘小于a[i]且在a[i]前面的，最大的数‘
单从这个定义考虑，

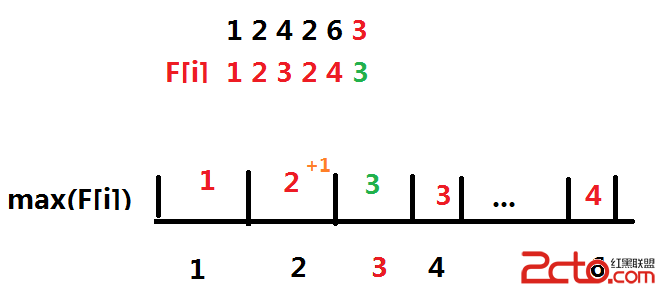
于是问题转化成-维护序列max（f[i])，每一次增加1个点的值，求[1,value_i)的最大值（若无值则为0）
不妨用一个zkw线段树维护（本题max(f[i])的长度=n，若没有这个条件时间会退化到O(nLogT)(T为a[i]的最大值），那么请把原序列排序O(nLogn)+离散化O(n),这样复杂度就有O(nLogT)降至O(nLogn)    ）.
程序1如下：
[cpp]
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<functional>
#include<algorithm>
using namespace std;
#define MAXN (40000+10)
#define NDEBUG
int t,n;
struct SegMentTree
{
    int a[MAXN*10],n;
    int M;
    SegMentTree(){}
    SegMentTree(int _n):n(_n)
    {
        M=1;
        while (M-2<n) M<<=1;
        memset(a,0,sizeof(a));
    }
    void insert(int _x,int c)
    {
        _x+=M;
        if (a[_x]<c)
        {
            a[_x]=c;
            for (_x>>=1;_x;_x>>=1) a[_x]=max(a[_x<<1],a[(_x<<1)^1]);
        }
    }
    int find(int l,int r)
    {
        int ans=0;
        l--;r++;
        l+=M;r+=M;
        while (l^r^1)
        {
            if (~l&1) ans=max(ans,a[l+1]);
            if (r&1) ans=max(ans,a[r-1]);
            l>>=1;r>>=1;
        }
        return ans;
    }
}a;
int main()
{
    #ifndef NDEBUG
    freopen("poj1631.in","r",stdin);
    #endif
    scanf("%d",&t);
    while (t--)
    {
        cin>>n;
        a=SegMentTree(n);
        for (int i=1;i<=n;i++)
        {
            int value;
            scanf("%d",&value);
            a.insert(value,a.find(1,value-1)+1);
        }
        printf("%d\n",a.find(1,n));

    }
    return 0;
}

算法2：
仔细观察推导序列求最大值部分，发现i总从1开始[1,value_i)
于是可二分查找序列Max[I]'=Max[ F[p] ] (1≤p≤i)

[delphi]
Program LCS;
var
   a,d,f:array[1..100000] of longint;
   n,i,j,len,test:longint;
function search(k:longint):longint;
var
   i,j,m:longint;
begin
   i:=1; j:=len;
   m:=d[(i+j) div 2];
   while (i<=j) do
   begin
      m:=(i+j) div 2;
      if (d[m]<k) and (d[m+1]>=k) then exit(m)
      else if (d[m]<k) then i:=m+1
      else j:=m-1;
   end;
end;
begin
   read(test);
   while (test>0) do
   begin
      read(n);
      len:=1;
      fillchar(d,sizeof(d),0);
      for i:=1 to n do read(a[i]);
      d[1]:=a[1];
      f[1]:=1;
      for i:=2 to n do
      begin
         if (a[i]>d[len]) then
         begin
            inc(len);
            d[len]:=a[i];
            f[i]:=len;
         end
         else if (a[i]<=d[1]) then
         begin
            d[1]:=a[i];
            f[i]:=1;
         end
         else
         begin
            j:=search(a[i]);
            d[j+1]:=a[i];&n

补充：综合编程 , 其他综合 ,