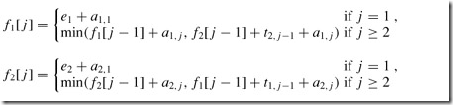《算法导论》学习总结 — 17.第15章 动态规划(2) 案例之装配线调度
原来打算把算法导论在7月份前搞定,现在已经过去一个多月了,才只看到第15章,后面也只零散看了一些,不知道假期前能否看完。。。够呛啊,马上要期末考试了,上学期GPA不到2,被学位警告了,虽说以后不学这个专业了,但起码成绩单上也不能有挂科是吧。。。要是平时一点不看,考前靠春哥,曾哥,关公哥都不行啊。。。这进度,郁闷!
尽力吧!
顺便还是说两句话:
1.有些书上分析的相当好了,我不想做画蛇添足的人,所以有的地方我会适当省略,当然也不是说我总结的地方就是书上讲的不好的地方,只是没人有一套自己的理解方式,我用自己的话去总结了,当时也就是最适合我的知识!所以,建议大家多写一些算法总结,你会体会到好处的!
2.而且我这个的性质是总结,不是对一个算法的具体讲解,所以不先看书,大家应该读不懂的,就比如下面,题目我就没有贴出来,大家不看数,肯定就读不懂,我的目的是大家看完书后,谢谢总结,或者看看别人写的总结,说不定可以发现自己哪些地方理解错了,哪些地方不理解,或是哪些地方值得探讨。
建议先看看前言:html">/kf/201104/87902.html
这一次主要是分析15.1节的例子—装配线调度问题。
题目有点长,首先得把题目读懂。
这个例子书上花了6面纸的篇幅来详细分析,由此可见其重要性。
谈到DP,不得不说的就是暴力法,大家都知道,如果用暴力解决类似问题,一般时间复杂度都是非常非常的高,这个时候救世主DP就出来了,DP以避免了许多重复的计算,而大大降低了时间复杂度。
按照书上的四个步骤,我在这里提取一些重点,建议还是把P194~196这四步完整步骤看书上的分析。只有慢慢品味,你才会发现《算法导论》的美。
步骤一:
分析问题,比如一个底盘要到达S[1][j],则有两种情况,第一种是从S[1][j-1]到S[1][j],第二种是从S[2][j-1]到S[1][j]。找出这两者所花时间的最小,则就是S[1][j]所需时间的最小。
这就是有局部最优解求全局最优解。也就是说,一个问题的最优解包含了子问题的一个最优解。我们称这个性质为最优子结构。这是是否可以应用DP的标志之一。
步骤二:
找出这个递归关系,由步骤一可以得到这个递归关系:
步骤三:
因为递归的关系,一般总是可以转换为非递归的算法。
由已知量f1[1], f2[1]逐步推出未知量,推啊推,推啊推,最后就推到结果了~~~~
步骤四:
再由已知结果返回求路径。
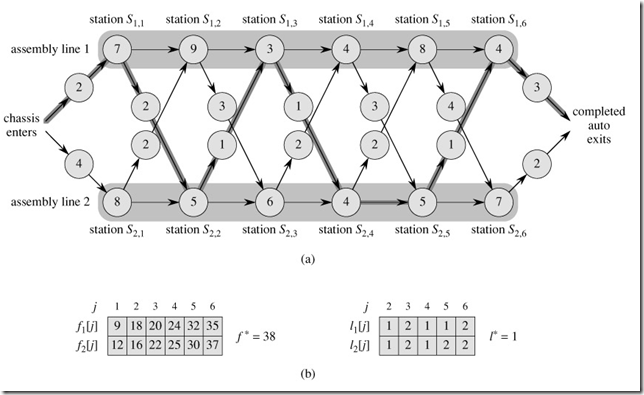
这一节最给力的就是这个例子以及相应的图:
拿起笔,用书上给出的例子,分析这个图!
以下是代码:
/*
Author: Tanky Woo
Blog: www.WuTianQi.com
About: 《算法导论》15.1 装配线调度
*/
#include <iostream>
using namespace std;
int n; // 一个装配线上有n个装配站
int e1, e2; // 进入装配线1,2需要的时间
int x1, x2; // 离开装配线1,2需要的时间
int t[3][100]; // t[1][j]表示底盘从S[1][j]移动到S[2][j+1]所需时间,同理t[2][j]
int a[3][100]; // a[1][j]表示在装配站S[1][j]所需时间
int f1[100], f2[100]; // f1[j], f2[j]分别表示在第一/第二条装配线上第j个装配站的最优解
补充:综合编程 , 其他综合 ,