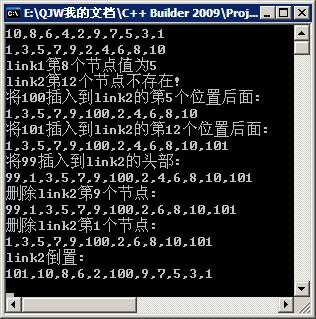
最小-最大堆的实现
[cpp]最小-最大堆的实现:
[cpp]
/*
最小最大堆的性质:
1. 对于在偶数深度上的任意节点X,存储在X上的关键字小于它的父亲但是大于它的祖父
2. 对于在奇数深度上的任意节点X,存储在X上的关键字大于它的父亲但是小于它的祖父
从其中可以推理出:
1.任意节点X,其关键字的值必定在它的父亲和其祖父之间,也就是说X所在的层上所有关键字
的值必定处于它的父亲层和它的祖父层之间
2.所有偶数层从根向下关键字的值递增,所有奇数层从根向下关键字的值递减
3.所有奇数层的关键字值大于偶数层的关键字值
4.如何判定一个节点X是在奇数层还是偶数层:就是判定X节点的祖父节点在奇数层还是偶数层,
递归的方法就可以实现,{ while(i>1) i/=4; if(i==1) 偶数层 ; if(i==0) 奇数层 ; } 其中
i是节点X的位置。时间复杂度是O(logN)
另外一种方法,根据3.如果X的节点值小于其父亲的节点值,则X在偶数层上,前提是X的值满足最大最小
堆的性质,同时X的值和其父亲的值不相等
5.一个最大最小堆的例子
1
/ \
19 15
/ \ / \
2 4 3 6
/ \ / \ / \ / \
16 18 9 10 7 12 13 14
/ \ / \
5 11 8 17
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct MinMaxStruct* MinMaxHeap;
typedef int Position;
typedef int ElementType;
#define MinElement 0
#define MaxElement 0x00ffffff
struct MinMaxStruct
{
int Capacity;
int Size;
ElementType* Elements;
};
static int
IsEmpty(MinMaxHeap H)
{
return H->Size ? 0 : 1;
}
static int
IsFull(MinMaxHeap H)
{
return H->Size == H->Capacity;
}
static MinMaxHeap
Initalize(int MaxElements)
{
MinMaxHeap H;
int Size;
Size = sizeof(struct MinMaxStruct) + (MaxElements + 1) * sizeof(ElementType);
H = malloc(Size);
if(H == NULL) return NULL;
H->Capacity = MaxElements;
H->Size = 0;
H->Elements = (ElementType*)(H + 1);
H->Elements[0] = MinElement;
return H;
}
static void
Destroy(MinMaxHeap H)
{
H->Capacity = 0;
H->Size = 0;
free(H);
}
/*
* 上滤:节点值从大变小的过程叫做上滤
* 上滤的过程包括从根开始向下的所有奇数层,转换到偶数层后
* 再从底部向上经历所有的偶数层
* 插入:在树的底端进行,要么经过上滤到偶数层上,要么
* 下滤到奇数层上
* 删除最大值:从堆的2或3的位置求出最大值,把对最后一个
* 数据放到最大值的位置,然后经过一个完整的上滤过程
* DecreaseKey:减小关键字的值,是将关键字位置减少后,对
* 其经历一个完整的上滤过程
*/
static Position
PercolateUp(Position i, MinMaxHeap H)
{
Position j = i;
ElementType X;
H->Elements[0] = MinElement;
X = H->Elements[i];
while(j>1) j = j >> 2;
/* 奇数层,先下滤,再上滤,偶数层直接上滤 */
if(j==0)
{
/* 下滤到一个奇数层上 */
for( ; i*4 < H->Size; i = j)
{
int k;
j = k = 4*i;
if(H->Size>=k+1 && H->Elements[j] < H->Elements[k+1]) j = k+1;
if(H->Size>=k+2 && H->Elements[j] < H->Elements[k+2]) j = k+2;
if(H->Size>=k+3 && H->Elements[j] < H->Elements[k+3]) j = k+3;
if(H->Elements[j] > X)
H->Elements[i] = H->Elements[j];
else
break;
}
H->Elements[i] = X;
/* 进行奇偶层互换,把偶数层上的一个最大值替换到奇数层上 */
j = i*2;
if(j < H->Size) //j的值最大可以是H->Size-1为偶数,H->Size是奇数值
{
if(H->Elements[j] < H->Elements[j+1]) j++;
}
else if(j > H->Size) j = i/2;
if(H->Elements[j] > X)
{
H->Elements[i] = H->Elements[j];
i = j;
}
else
return i;
}
/* 上滤 */
fo
补充:软件开发 , C++ ,上一个:C++内存分区
下一个:嵌入式系统中的代码压缩
- 更多C/C++疑问解答:
- 关于c++的cout输出的问题。
- 在学校里学过C和C++,不过学的很一般,现在自学C#,会不会很难?
- 全国计算机二级C语言笔试题
- 已知某树有2个2度结点,3个3度结点,4个4度结点,问有几个叶子结点?
- c++数据结构内部排序问题,整数排序
- 2012九月计算机二级C语言全国题库,,急求急求
- 如果assert只有一个字符串作为参数,是什么意思呢?
- C语言中,哪些运算符具有左结合性,哪些具有右结合性,帮忙总结下,谢谢了!
- 为什么用结构体编写的程序输入是,0输不出来啊~~~
- 将IEEE—754的十六进制转化为十进制浮点类型,用C或C++都行,多谢各位大侠啊,非常感谢!
- 为什么这个程序求不出公式?
- 这个链表倒置的算法请大家分析下
- c语言函数库调用
- C语言unsigned int纠错
- C语言快排求解啊