LA - 4043 - Ants

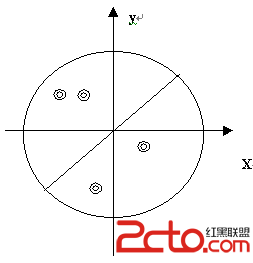
题意：n只蚂蚁，n棵树，每只蚂蚁要连一棵树，连线（直线）不能相交，给出n只蚂蚁和n棵树的坐标，输出n只蚂蚁所配对的树的编号(1 <= n <= 100, -10000 <= 坐标x, y <= 10000)。

——>>二分图最佳完美匹配第一题，挺简单，也挺容易写错。

很明显，蚂蚁为一个顶点集，树为一个顶点集，如果从蚂蚁向树匹配，那么最后输出前要先做一次o(n)的映射，如果从树向蚂蚁匹配，则最后可直接输出。

建图：以n棵树为X点，以n只蚂蚁为Y点，权值w[i][j]为树i到蚂蚁j的距离的相反数（二分图最佳完美匹配求的是权和最大，而我们要的是权和最小（这样就不会有线段相交），所以权值取了相反数后变成了求二分图的最大完美匹配），跑一次KM就好。

#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int maxn = 100 + 10;
const double eps = 1e-10;

int n, fa[maxn];
double w[maxn][maxn], Lx[maxn], Ly[maxn];
bool S[maxn], T[maxn];

struct Point{
    double x, y;
    Point(double x = 0, double y = 0):x(x), y(y){}
};

Point ant[maxn], tree[maxn];

double Dis(Point A, Point B){
    return sqrt((A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-B.y));
}

bool match(int i){
    S[i] = 1;
    for(int j = 1; j <= n; j++) if(fabs(Lx[i]+Ly[j]-w[i][j]) < eps && !T[j]){
        T[j] = 1;
        if(!fa[j] || match(fa[j])){
            fa[j] = i;
            return 1;
        }
    }
    return 0;
}

void update(){
    double a = 1 << 30;
    for(int i = 1; i <= n; i++) if(S[i])
        for(int j = 1; j <= n; j++) if(!T[j])
            a = min(a, Lx[i]+Ly[j]-w[i][j]);
    for(int i = 1; i <= n; i++){
        if(S[i]) Lx[i] -= a;
        if(T[i]) Ly[i] += a;
    }
}

void KM(){
    for(int i = 1; i <= n; i++) fa[i] = Lx[i] = Ly[i] = 0;
    for(int i = 1; i <= n; i++){
        while(1){
            for(int j = 1; j <= n; j++) S[j] = T[j] = 0;
            if(match(i)) break;
            else update();
        }
    }
}

int main()
{
    int first = 1;
    while(scanf("%d", &n) == 1){
        for(int i = 1; i <= n; i++) scanf("%lf%lf", &ant[i].x, &ant[i].y);
        for(int i = 1; i <= n; i++) scanf("%lf%lf", &tree[i].x, &tree[i].y);
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                w[i][j] = -Dis(tree[i], ant[j]);        //计算树i与蚂蚁j的距离，并用其相反数作权值
        KM();
        if(first) first = 0;
        else puts("");
        for(int i = 1; i <= n; i++) printf("%d\n", fa[i]);
    }
    return 0;
}

补充：软件开发 , C++ ,