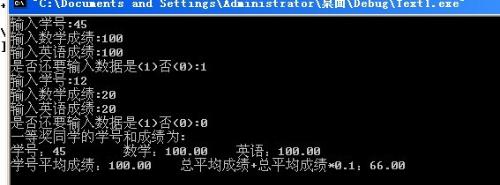
ural 1165 subnumber ------易做图的超级大繁题

1165. Subnumber
Time Limit: 1.0 second
Memory Limit: 16 MB
George likes arithmetics very much. Especially he likes the integers series. His most favourite thing is the infinite sequence of digits, which results as the concatenation of all positive integers in ascending order. The beginning of this sequence is 1234567891011121314… Let us call this sequence S. Then S[1] = 1, S[2] = 2, …, S[10] = 1, S[11] = 0, …, and so on.
George takes a sequence of digits A and wants to know when it first appears in S. Help him to solve this difficult problem.
Input
The first line contains A - the given sequence of digits. The number of digits in A does not exceed 200.
Output
Output the only number - the least k such that A[1] = S[k], A[2] = S[k+1], ... A[len(A)] = S[k + len(A) – 1], where len(A) denotes the length of A (i.e. the number of digits in it).
Sample
input output
101
10

无敌的繁题啊！！！！！！！

200位，写了个高精度模版。。。

debug了一天。。代码冗长无比，而且到处都是陷阱，比如前导0等等。。。

但还是艰难AC了。。。

贴出代码：（7.8KB）

[cpp]
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;

class BigNum
{
private:
    enum {blen=4,MAX=53,base=10000};
    int len;
    int a[MAX];
public:
    explicit BigNum(int num=0);
    BigNum(const BigNum& b);
    BigNum(int x,int b);
    explicit BigNum(string num);
    BigNum operator+ (const BigNum& b)const;
    BigNum operator+ (const int b)const;
    BigNum operator- (const BigNum& b)const;
    BigNum operator- (const int b)const;
    BigNum operator* (const BigNum& b)const;
    BigNum operator* (const int b)const;
    const int& operator[] (int i)const;
    int& operator[] (int i);
    bool operator< (const BigNum& b)const;
    bool operator> (const BigNum& b)const;
    bool operator== (const BigNum& b)const;
    bool operator!= (const BigNum& b)const;
    string toString()const;
    friend ostream& operator<< (ostream& os,const BigNum& a);
};

BigNum::BigNum(int num)
{
    if (num==0)
    {
        len=0;
        memset(a,0,sizeof(a));
        return;
    }
    len=0;
    memset(a,0,sizeof(a));
    while (num>0)
    {
        a[len++]=num%base;
        num/=base;
    }
}

BigNum::BigNum(int x,int b) // x*10^b
{
    if (x==0)
    {
        len=0;
        memset(a,0,sizeof(a));
        return;
    }
    len=(b+1)/blen+1;
    if ((b+1)%blen==0) len--;
    memset(a,0,sizeof(a));
    int i=b%blen,j=1;
    while (i>0)
    {
        j*=10;
        i--;
    }
    a[len-1]=x*j;
}

BigNum::BigNum(string num)
{
    const int nn[blen]={1,10,100,1000};
    if (num==string(num.size(),'0'))
    {
        len=0;
        memset(a,0,sizeof(a));
        return;
    }
    memset(a,0,sizeof(a));
    len=0;
    for (int i=0;i<num.size();i++)
    {
        if (i%blen==0) len++;
        a[len-1]+=(num[num.size()-i-1]-'0')*nn[i%blen];
    }
}

BigNum::BigNum(const BigNum& b)
{
    len=b.len;
    memcpy(a,b.a,sizeof(b.a));
}

int& BigNum::operator[](int i)
{
    return a[i];
}

const int& BigNum::operator[](int i)const
{
    return a[i];
}

BigNum BigNum::operator+(const BigNum& b)const
{
    BigNum c=BigNum();
    int k=0;
    c.len=max(len,b.len);
    for (int i=0;i<c.len;i++)
    {
        c[i]=(a[i]+b[i]+k)%base;
        k=(a[i]+b[i]+k)/base;
    }
    while (k>0)
    {
        c[c.len++]=k%base;
        k/=base;
    }
    return c;
}

BigNum BigNum::operator+(const int b)const
{
    BigNum c=*this;
    int i=0;
    c[0]+=b;
    while (c[i]>=base)
    {
        c[i+1]+=c[i]/base;
        c[i]%=base;
        i++;
    }
    while (c[c.len]>0) c.len++;
    return c;
}

BigNum BigNum::operator-(const BigNum& b)const //ensure that a>b
{
    BigNum c=BigNum();
    c.len=max(len,b.len);
    int k=0;
    for (int i=0;i<len;i++)
        if (a[i]-b[i]-k>=0)
            c[i]=a[i]-b[i]-k;
        else
&nb

补充：软件开发 , C++ ,