《算法导论》学习总结 — 11. 第12章 二叉查找树
推荐在看算法导论的这一章之前先看看严蔚敏老师在《数据结构》上的二叉查找树。
整体来说二叉查找树不难,就是插入和删除节点时让人纠结,我就是在删除节点时各种纠结了。
二叉树执行基本操作的时间与树的高度成正比。
首先说下二叉查找树的性质:
设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]。
注意这个性质,和堆对比下,还是有区别的,并且这个性质表示二叉查找树的根节点的左子树中所有结点都小于根结点,所有右子树的结点都大于根结点。所以根据这个性质,可以用中序访问二叉查找数来实现从小大到排列。
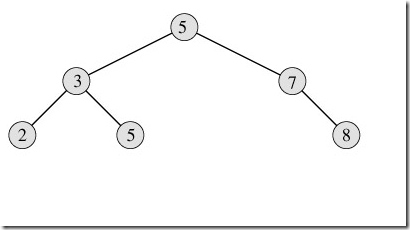
首先看看这个二叉查找树(P151图12-1(a)):
图1
按中序遍历结果为:
2->3->5->5->7->8
接下来说说二叉查找树的几个操作:
SEARCH:查找关键字等于key的结点
MINIMUM:找出关键字最小的结点
MAXIMUM:找出关键字最大的结点
SUCCESSOR:找出结点x的后继y
INSERT:在二叉查找树中插入结点z
DELETE:在二叉查找树中删除结点z
里面就INSERT和DELETE麻烦一些。
首先逐步分析代码:
①.BST的数据结构:
typedef struct Node{
int key;
Node *lchild, *rchild, *parent;
}Node, *BSTree;
②.BST的中序遍历:
根据BST的性质,对于一个根结点x,所以比x小的结点都在x的左子树中,所有比x大的结点都在x的右子树中,并且没一个结点都满足这个性质,所以可以利用中序遍历,按从小到大的顺序输出这个BST。
代码如下:
// 递归版本
Node * BSTreeSearch(BSTree T, int k)
{
if(T == NULL || k == T->key)
return T;
if(k < T->key)
return BSTreeSearch(T->lchild, k);
else
return BSTreeSearch(T->rchild, k);
}
// 非递归版本
BSNode * IterativeBSTreeSearch(BSTree T, int k)
{
while(T != NULL && k != T->key)
{
if(k < T->lchild->key);
x = T->lchild;
else
x = T->rchild;
}
return x;
&
补充:综合编程 , 其他综合 ,