hdu 4353 计算几何

题意：
给你n个点，m个雷
找一个多边形，使得多边形的面积除以这个多边形内雷的个数的比值最小
仔细想想，其实就是找一个比值最小的三角形就OK了，因为其他的三角形的比值都比它大，组合成多边形后势必会将比值变大
所以可以直接暴力O(n^3)枚举三角形，再计算三角形内的雷的个数求比值即可
雷得个数的话预处理一个数组吧，画张图就懂了

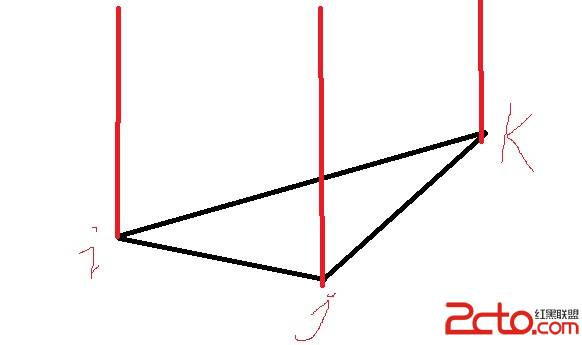
cnt= （i k上方的点）- （ i j上方的点 +    j k上方的点）
当然还要取绝对值
[cpp]
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
using namespace std;
struct Point {
     int x,y;
     bool operator < (const Point &cmp) const{
         return x<cmp.x;
     }
}p[210],mine[510];
inline int XX(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
int n,m;
int num[210][510];
void gao(Point a,Point b,int &cnt)
{
    int x1=a.x,x2=b.x;
    for(int i=0;i<m;i++) if(x1<=mine[i].x && mine[i].x<x2)//注意边界，一边是开区间
    if(XX(a,b,mine[i])>0)
        cnt++;
}
int main()
{
    int t,ca=1;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++) scanf("%d%d",&p[i].x,&p[i].y);
        sort(p,p+n);
        for(int i=0;i<m;i++) scanf("%d%d",&mine[i].x,&mine[i].y);
        for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)         gao(p[i],p[j],num[i][j]=0);
        double ans=-1;
        for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)for(int k=j+1;k<n;k++)
        {
            int cnt=num[i][k]-num[i][j]-num[j][k];
            if(cnt==0) continue;
            double area=(double)XX(p[i],p[j],p[k])/2;
            if(ans==-1 || fabs(area/cnt)<ans) ans=fabs(area/cnt);
        }
        if(ans!=-1) printf("Case #%d: %.6lf\n",ca++,ans);
        else printf("Case #%d: -1\n",ca++);
    }
    return 0;

}

补充：软件开发 , C++ ,