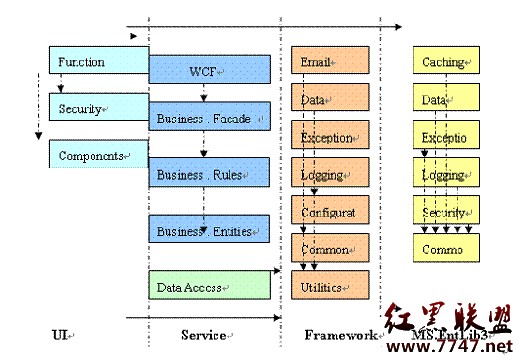
图像处理中消除相机透镜畸变和视角变换

一般的针孔相机模型如下：

三维坐标点经过透视投影变换，转换到一个图像平面坐标点。

而相机透镜还存在一定的畸变，包括横向畸变和切向畸变。

因此，针孔相机模型又被扩展为以下模型：

首先，世界坐标被转换为相机坐标，由X,Y,Z到x，y，z；

然后，归一化，z=1处，x，y的投影坐标x`,y`；

接下来，对投影坐标，进行畸变处理；

最后，由相机坐标转换到图像坐标。

在使用广角镜头或鱼眼相机时，原始图像存在畸变比较严重。

在图像识别的很多应用场景中，消除图像的畸变是图像预处理的首要问题。

通过相机标定，很容易拿到相机的内部参数，包括焦距、光心和畸变系数。

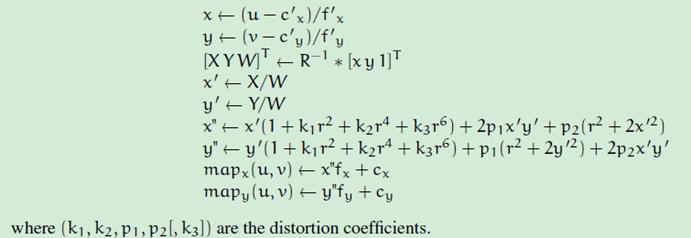
以上过程，就是透镜畸变前后图像坐标变换的公式。具体步骤如下：

1. 由图像坐标系反变换到相机坐标系中

2. 然后，校正反变换R-1，一般无校正变换的相机，默认为单位矩阵

3. 归一化，并进行相机透镜畸变处理

4. 由相机坐标转换到图像坐标。

由此，得到由针孔模型到透镜畸变畸变模型相互变换的对应关系u <--> mapx, v <--> mapy

initUndistortRectifyMap函数就是完成了以上工作。

opencv中，remap与undistortion都是消除畸变的函数，undistortion在设置了一些参数后调用了remap函数，二者的算法实质是一样的。由目标图像的坐标，找到对应的原始图像坐标，然后将其值复制到目标图像。大致思路是如此，由于图像大小和变换，需要插值或近似的方法，如最邻近法、线性插值等

图像视角变换

如图像由前向视角frontview转换为俯视角birdview。

一般来讲，相机向下倾斜时，相机前向视角frontview的视角范围比较大，而俯视birdview需要的视角比较小（涉及地面的视角部分）。

针孔模型下，在前向视角图像中，截取涉及地面的部分，并通过透视变换，转换为俯视视角。地面的一个矩形区域，在前向视图中会大致是一个三角形或梯形的形状，而在俯视图中，仍是一个矩形图像，且能保留线性、平行性特征。

如下，一个前向广角视图，转换为俯视图。

前向视图：

俯视图：

转换方法:

首先，通过标定获取相机的外部参数，世界坐标系中相机的位置Position和倾角（相对于x，y，z坐标轴的角度），即M=R|t。并假定地面的z坐标为z=0.

然后，获取俯视图内的三维地面坐标。z=0，地面区域的实际大小与俯视图的大小成一定比例，即俯视图中一个像素的位置(u`,v`)，在地面坐标上，也有对应的位置(x`, y`, 0)。

然后，通过相机模型，将每个地面位置坐标(x`,y`, 0)转换为前向视图中的坐标(u, v)。

此时，前向视图像与俯视图像有一个对应关系(u,v) <--> (u`,v`)。

通过对应关系，每个俯视图的像素都在前向视图像中有对应的位置，两者的像素值相等（使用最邻近法或线性插值等）。俯视图前方的部分边缘模糊比较严重，这是在原图中采样范围小的原因。

补充：综合编程 , 其他综合 ,