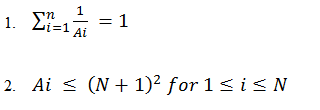幸运号码-dp

题目：

时间限制：1 秒空间限制：65536 KB 分值: 20

1个长度为2N的数，如果左边N个数的和 = 右边N个数的和，那么就是一个幸运号码。

例如：99、1230、123312是幸运号码。

给出一个N，求长度为2N的幸运号码的数量。由于数量很大，输出数量 Mod 10^9 + 7的结果即可。

Input

输入N(1<= N <= 1000)

Output

输出幸运号码的数量 Mod 10^9 + 7

Input 示例

Output 示例

题目分析：

N比较小，仔细分析一下题目，有点像动态规划。想了好久没整明白递推方程，没有完整的写出来，更解决不了这道题目。

在qq上问了一下，一个人很快就列出了动态方程太牛了，然后自己分析了一下，没有问题，结果代码实现，最终也是没有问题，

这道题目，不能直接求出答案，需要分两步：第一步，先求出n位数，和为s的情况种数。这个相信很多人能够列出状态方程，类似于背包吧，

dp[n][s]表示n位，和为s的号码个数，方程为dp[n][s] = 求和（dp[n-1][s-i],i=[0,9]）什么意思呢？也就是当第n位为0-9时，和为s的种类和n-1位，和为s减去0-9的种类有关，是求和的关系。

那么得到了上面的结果后，如何求得N位的幸运号码呢？N位，和为s的种类数知道了，但是2N位要求前N位的首位不能为0，而后N位无所谓，那么首位不为0的个数怎么确定呢，这里有个很巧妙的办法，就是dp[n][s] - dp[n-1][s]这就是第n位为0的情况，那么有了这个就直接可以求出所有的幸运号码了就是dp[n][s]*(dp[n][s] - dp[n-1][s]),s=[0,9*N],求和就是结果。

有了这些分析，就能够写程序了，注意，这里第n位只和第n-1位有关，所以只需要开辟一个2*N*9的空间就行了，滚动数组，并且要int64，否则会溢出。

下面就直接是代码了，好好体会动态规划的分析过程，为何自己第一时间想不到。。。。很感谢这位好友，这里分享一下思路，以作总结啦。

代码：

#include <iostream>  
#include <cstdlib>  
#include <cstring>  
//#include <Windows.h>  
using namespace std;  
const int MAXN = 1010;  
const int MAX = 1000000007;  
  
__int64 dp[2][9*MAXN];  
  
int main()  
{  
    int N;  
    while (cin >> N)  
    {  
        //int time = GetTickCount();  
        memset(dp,0,sizeof(dp));  
        dp[1][0] = 1;  
        for (int i = 0; i <= 9; ++ i)  
        {  
            dp[0][i] = 1;  
        }  
        for (int i = 1; i < N; ++ i)  
        {  
            for (int s = 0; s <= 9 * (i+1); ++ s)  
            {  
                __int64 sum = 0;  
                for (int j = 0; j <= 9; ++ j)  
                {  
                    if (s >= j)  
                    {  
                        sum = (sum + dp[(i - 1)%2][s - j])%MAX;  
                    }  
                    else  
                        dp[i%2][s] = 0;  
                }  
                dp[i%2][s] = sum;  
            }  
        }  
        __int64 ans = 0;  
        for (int i = 0; i <= N * 9; ++ i)  
        {  
            ans = (ans + dp[(N+1)%2][i]*(dp[(N+1)%2][i] - dp[N%2][i]))%MAX;  
        }  
  
        cout << ans << endl;  
    }  
}

补充：软件开发 , C++ ,