算法复杂性分析

 

算法复杂度主要体现在运行该算法所需要的计算机资源的多少上。计算机的资源最重要的是时间和空间（存储器）资源，所以，算法的复杂性有时间复杂度以及空间复杂度之分。这两个量集中反映了算法的效率，而从具体运行该算法的计算机中抽象出来。毫无疑问，一个好的算法，追求的是更少的资源，出色的完成问题。换言之，就是时间复杂度尽可能低，空间复杂度也尽可能低。但这两个家伙往往是唱对台的，时间复杂度低的代价一般是空间复杂度高，反之亦然。不过，在存储硬件白菜价的这个年代，我们更多地追求时间复杂度。当然，具体情况具体考虑，但一般都会优先考虑时间复杂度。时间复杂性与空间复杂性概念雷同，计量方法相似，这里重点讨论时间复杂度。

 

在介绍时间复杂度之前，我们先引入几个概念。

 

首先，设f(N)和g(N)是定义在正整数上的正函数。

 

如果存在正的常数C和自然数N。,使得当N≧N。时有f(N) ≦Cg(N)，则称函数f(N)当N充分大时上有界，且g(N)是它的一个上界，记为f(N)=O(g(N))。这时还说f(N)的阶不高于g(N)的阶。

 

如果存在正的常数C和自然数N。，使得当N≥N。时，有f(N) ≧Cg(N)，则称函数f(N)当N充分大时下有界，且g(N)是它的一个下界，记为f(N)= Ω(g(N))。这时还说f(N)的阶不低于g(N)的阶。显然上界与下界的概念是相对的。

 

再来看下同阶的概念。当f(N)=O(g(N))且f(N)= Ω(g(N))时，我们称f(N)与g(N)同阶。记为f(N)= θ(g(N))

 

没打错吧，数学概念的东西要严谨。学过高等数学的应该能很好理解上面的概念吧，学过数学分析的就更轻松了。额，觉得困难的只要理解第一条上界就好。

 

时间复杂度一般指考虑三种，即最坏情况，最好情况和平均情况。这三种情况都从某种角度反映出算法的效率，各有各的好处，但同时也有各自的局限性。实践证明，可操作性最好且最有价值的是最坏情况下的时间复杂性。而上界的概念跟最坏情况下的时间复杂性有着很大的关联，聪明的你应该可以想到吧。唔，当然，这个上界的阶越低则评估越准确，结果就越有价值。而下界嘛，也可以用来评估算法的时间复杂性，常常与符号O配合以证明某问题的一个特定算法是该问题的最优算法或该问题的某算法类中的最优算法。类似地，这个下界的阶越高，则评估越准确，结果就越有价值。

 

好吧，将上界的概念移到了前面是为了更早一步接触大O，但是想要更进一步理解大O算法，这里还需要再引入复杂性渐近形态的概念：

 

设T(N)是算法A的复杂性函数。一般来说，当N单调增加且趋于∞时，T(N)也将单调增加趋于∞。对于T(N)，如果存在使得当N->∞时，有那么就说是T(N)当N->∞时的渐近性态，或者称为算法A当N->∞时的渐近复杂性而与T(N)相区别。

 

直观上来说吧，是T(N)略去低阶项所留下的主项，因为在趋于无穷时，高阶变化的速度远远大于低阶，所以可以将低阶的略去。唔！从直观上看来，它的确是比T(N)要简单得多。

 

由于当N->∞时，T(N)渐近于，有理由用来代替T(N)作为算法A在N->∞时的复杂性的度量。而且比T(N)明显简化得多，所以这种代替是对算法复杂性分析的一种简化。进一步吧，考虑到分析算法复杂度的目的在于比较求解同一个问题的两个不同算法的效率。而比较的两个算法的渐近复杂性的阶不相同时，只要能确定出各自的阶，就可以判定哪一个算法的效率高了。换句话说，这时的渐进复杂性分析只要关心的阶就够了，不必关心包含在中的常数因子。所以，常常又对

的分析进一步简化，即假设算法中用到的所有不同的元运算各执行一次所需要的时间都是一个单位时间。

 

这里我们再来看看符号O的运算规则：

(1) O(f) + O(g) = O(max(f,g));

(2) O(f) + O(g) = O(f + g);

(3) O(f)O(g) = O(fg);

(4)如果g(N) = O(f(N))，则O(f) + O(g)= O(f);

(5) O(Cf(N)) = O(f(N))，其中C是一个正的常数；

(6) f=O(f)

 

我觉得精华是上面这个演绎，知其然不知其所以然，另外还得说一下，按照上面计算出来的是渐近时间复杂度，简称时间复杂度，当然我们一般求的也就是这个了。以前见到一些例如O(n),O(nlogn)之类的算法复杂度，之所以不明白，就是因为不知道为什么没看过上面的过程，恨之晚矣。好了，其实都是有依据的，以前见到一个循环就是O(n)，两个嵌套就是平分阶……其实都是可以算的。

 

好吧，我承认我列这么多东西在这里大大地加深了大家的迷惑，但我觉得上面的真的很有必要去理解下，我在很多书里面都没有看到上面的解析的，让我大感郁闷。下面我们来简略的再次整理下吧，上面的看不懂？没关系，按照下面的做就得了，改天回头再看看前面的。下面的部分信息百度出来的，懒得写了。

 

根据各种概念定义，可以归纳出基本的计算步骤： 

 

1. 计算出基本操作的执行次数T(n) 

    基本操作即算法中的每条语句（以;号作为分割），语句的执行次数也叫做语句的频度。在做算法分析时，一般默认为考虑最坏的情况。

 

2. 计算出T(n)的数量级 

    求T(n)的数量级，只要将T(n)进行如下一些操作：

    忽略常量、低次幂和最高次幂的系数

 

    令f(n)=T(n)的数量级。

 

3. 用大O来表示时间复杂度 

    当n趋近于无穷大时，如果lim(T(n)/f(n))的值为不等于0的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。

 

下面我们简单地来看看实例分析吧。

例1： 

 

 

int num1, num2;  
for(int i=0; i<n; i++)  
{   
     num1 += 1;  
     for(int j=1; j<=n; j*=2)  
          {   
         num2 += num1;  
     }  
 }   

 

 

分析：

1.

语句int num1, num2;的频度为1；

语句i=0;的频度为1；

语句i<n; i++; num1+=1; j=1; 的频度为n；

语句j<=n; j*=2; num2+=num1;的频度为n*log2n；

T(n) = 2 + 4n + 3n*log2n

 

2.

忽略掉T(n)中的常量、低次幂和最高次幂的系数

f(n) = n*log2n

 

3.

lim(T(n)/f(n)) = (2+4n+3n*log2n) / (n*log2n)

                    = 2*(1/n)*(1/log2n) + 4*(1/log2n) + 3

 

当n趋向于无穷大，1/n趋向于0，1/log2n趋向于0

所以极限等于3。

 

T(n) = O(n*log2n)

 

简化的计算步骤 

 

再来分析一下，可以看出，决定算法复杂度的是执行次数最多的语句，这里是num2 += num1，一般也是最内循环的语句。

 

并且，通常将求解极限是否为常量也省略掉？

 

于是，以上步骤可以简化为： 

 

1. 找到执行次数最多的语句 

2. 计算语句执行次数的数量级

3. 用大O来表示结果 

 

继续以上述算法为例，进行分析：

1.

执行次数最多的语句为num2 += num1

 

2.

T(n) = n*log2n

f(n) = n*log2n

 

3.

// lim(T(n)/f(n)) = 1

T(n) = O(n*log2n)

 

 

 

最后，列出几个比较有用的递归分治的时间复杂度计算公式吧。

 

 

 

 

 

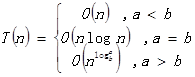
补充：软件开发 , C++ ,