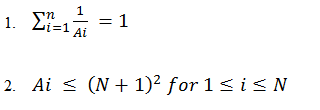poj 2065 SETI

题意比较纠结，搜索了把题意。
   给你一个素数P(P<=30000)和一串长为n的字符串str[]。字母'*'代表0，字母a-z分别代表1-26，这n个字符所代表的数字分别代表
f(1)、f(2)....f(n)。定义: f (k) = ∑0<=i<=n-1aiki (mod p) (1<=k<=n,0<=ai<P)，求a0、a1.....an-1。题目保证肯定有唯一解。
   解题思路：高斯消元。根据上面的公式显然可以列出有n个未知数的n个方程式：
   a0*1^0 + a1*1^1+a2*1^2+........+an-1*1^(n-1) = f(1)
   a0*2^0 + a1*2^1+a2*2^2+........+an-1*2^(n-1) = f(2)
   ..............
   a0*n^0 + a1*n^1+a2*n^2+........+an-1*n^(n-1) = f(n)
   然后采用高斯消元法来解上面的方程组即可。
   典型的高斯消元题，只是多了个modP，因此计算过程中可能需要扩展欧几里德算法。

   说下所谓的高斯消元的思路，其实可以参看易做图，
http://zh.易做图.org/wiki/%E9%AB%98%E6%96%AF%E6%B6%88%E5%8E%BB%E6%B3%95，大致过程是一直消变量。
比如刚开始，消第一个变量，消完之后只让第一个方程含有第一个变量，然后消第二个变量，消完之后只让第二个方程含第二个变量，以此
下去让最后的方程含最后一个变量，而且最后一个方程中对于前N-1个变量的系数都是0，这样就能解出这N个变量了。
   关于自由元指的是这个变量可以取任何值，得出这样的结论是在消变量的过程中发现该变量的在第row个方程到第N方程中的系数都是0了，
所以可以取任何值。判断无解的方式是，第row+1到第N个方程在高斯消元之后所有的系数必定是0，所以方程的值也必须是0。
   求方程的解得过程是从N个解开始逆推，第N-1个方程也就包含2个变量了，第N个变量和第N-1个变量，以此下去，就可以解出方程组了。
   具体的可以参照易做图和代码仔细分析。还有演算法笔记上也有高斯消元的解释。

代码如下：
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define MAX (70 + 10)

int nMatrix[MAX][MAX];
int nAns[MAX];
void InitMatrix(char* szStr, int nN, int nP)
{
    memset(nMatrix, 0, sizeof(nMatrix));
    for (int i = 0; i < nN; ++i)
    {
        nMatrix[i][nN] = (szStr[i] == '*' ? 0 : szStr[i] - 'a' + 1);
    }
    for (int i = 0; i < nN; ++i)
    {
        int nTemp = 1;
        for (int j = 0; j < nN; ++j)
        {
            nMatrix[i][j] = nTemp;
            nTemp = (nTemp * (i + 1)) % nP;
        }
    }
}

int e易做图(int nA, int nB, int& nX, int& nY)
{
    if (nA < nB)swap(nA, nB);
    if (nB == 0)
    {
        nX = 1, nY = 0;
        return nA;
    }
    int nRet = e易做图(nB, nA % nB, nX, nY);
    int nT = nX;
    nX = nY;
    nY = nT - (nA / nB) * nY;
    return nRet;
}

int Gauss(int nN, int nP)
{
    int nR, nC;
    for (nR = nC = 0; nR < nN && nC < nN; ++nR, ++nC)
    {
        if (nMatrix[nR][nC] == 0)
        {
            for (int i = nR + 1; i < nN; ++i)
            {
                if (nMatrix[i][nC])
                {
                    for (int j = nC; j <= nN; ++j)
                    {
                        swap(nMatrix[nR][j], nMatrix[i][j]);
                    }
                    break;
                }
            }
        }

        if (nMatrix[nR][nC] == 0)
        {
            nR--;    //自由元
            continue;
        }
        int nA = nMatrix[nR][nC];
        for (int i = nR + 1; i < nN; ++i)
        {
            if (nMatrix[i][nC])
            {
                int nB = nMatrix[i][nC];
                for (int j = nC; j <= nN; ++j)
                {
                    nMatrix[i][j] = (nMatrix[i][j] * nA - nMatrix[nR][j] * nB) % nP;
                }
            }
        }
    }
    for (int i = nR; i < nN; ++i)
    {
        if (nMatrix[i][nN])
        {
            return -1;//无解
        }
    }

    int nX, nY;
    for (int i = nN - 1; i >= 0; i--)
    {
        int nSum = 0;
        for (int j = i + 1; j < nN; ++j)
        {
            nSum = (nSum + nMatrix[i][j] * nAns[j]) % nP;
        }

        nSum = (nMatrix[i][nN] - nSum + nP * nP) % nP;

        e易做图(nP, (nMatrix[i][i] + nP) % nP, nX, nY);
        nY = (nY + nP) % nP;
        nAns[i] = (nY * nSum + nP) % nP;//第i个解

补充：软件开发 , C++ ,