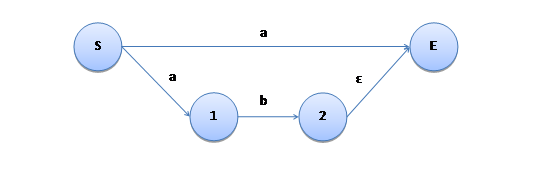
hdu 1392凸包周长
//用的自己的计算几何模板,不过比较慢嘿嘿
//要注意只有一个点和两个点
//Computational Geometry
//by kevin_samuel(fenice) Soochow University
//temple
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
//#include <stack>
using namespace std;
//define
const double EPS = 1e-8;
const double PI = acos(-1.0);
//point
//====================================================================
class Point
{
public:
double x;
double y;
Point(){}
Point(double x,double y):x(x),y(y){}
//operator
//operator=
Point& operator=(const Point& _P)
{
x = _P.x;
y = _P.y;
return *this;
}
//operator*
double operator*(const Point& _P)const
{
return x*_P.y - y *_P.x;
}
//operator-
Point operator-(const Point& _P)const
{
return Point(x - _P.x,y - _P.y);
}
//operator==
bool operator==(const Point& _P)const
{
if(fabs(_P.x - x) < EPS && fabs(_P.y - y) < EPS)
return true;
else
return false;
}
bool operator!=(const Point& _P)const
{
return ((*this) == _P) == false;
}
//dot product
static double dotProduct(Point s1,Point e1,Point s2,Point e2)
{
double result = 0;
double x1 = e1.x - s1.x;
double y1 = e1.y - s1.y;
double x2 = e2.x - s2.x;
double y2 = e2.y - s2.y;
result = x1*x2 + y1*y2;
return result;
}
//cross product 1 (4 point-type params)
static double crossProduct(Point s1,Point e1,Point s2,Point e2)
{
double result = 0;
double x1 = e1.x - s1.x;
double y1 = e1.y - s1.y;
double x2 = e2.x - s2.x;
double y2 = e2.y - s2.y;
result = x1*y2 - x2*y1;
return result;
}
//cross product 2 (3 point-type params)
static double crossProduct(Point p1,Point p2,Point p0)
{
return crossProduct(p0,p1,p0,p2);
}
//Is on segment or line
static bool onSegment(Point Pi,Point Pj,Point Q)
{
if(Q.x >= min(Pi.x,Pj.x) && Q.x <= max(Pi.x,Pj.x) &&
Q.y >= min(Pi.y,Pj.y) && Q.y <= max(Pi.y,Pj.y) &&
fabs(crossProduct(Q,Pj,Pi)) < EPS
)
return true;
else
return false;
}
//Is on segment
bool IsOnSegment(Point Pi,Point Pj)
{
if(this->x >= min(Pi.x,Pj.x) && this->x <= max(Pi.x,Pj.x) &&
this->y >= min(Pi.y,Pj.y) && this->y <= max(Pi.y,Pj.y) &&
fabs(Point::crossProduct(*this,Pj,Pi)) < EPS
)
return true;
else
return false;
}
//Is inside 易做图
bool inTriangle(Point A,Point B,Point C)
{
double Sabc = fabs(Point::crossProduct(B,C,A));
double Spab = fabs(Point::crossProduct(A,B,(*this)));
double Spac = fabs(Point::crossProduct(A,C,(*this)));
double Spbc = fabs(Point::crossProduct(B,C,(*this)));
if(Spbc + Spab + Spac == Sabc)
return true;
else
return false;
}
//Is inside polygon
//polys[] ,0-n
bool insidePolygon(Point *polys,int n)
{
int counter = 0;
double xinters;
Point p1,p2;
p1 = polys[0];
for(int i = 1; i < n; i++)
{
p2 = polys[i % n];
if(Point::onSegment(p1,p2,(*this)) == true)
return true;
if((*this).y > min(p1.y,p2.y) && (*this).y <= max(p1.y,p2.y))
{
if((*this).x <= max(p1.x,p2.x) && p1.y != p2.y)
{
xinters = ((*this).y - p1.y)*(p2.x - p1.x)/(p2.y - p1.y) + p1.x;
if(p1.x == p2.x || (*this).x <= xinters)
counter++;
}
}
p1 = p2;
}
if(counter % 2 == 0)
return false;
return true;
}
//distance^2
double dis2(const Point& _P)const
{
return (x - _P.x)*(x - _P.x) + (y - _P.y)*(y - _P.y);
}
//distance
double dis(const Point& _P)const
{
return sqrt(dis2(_P));
}
static double dis(const Point& p1,const Point& p2)
{
return sqrt((p2.x - p1.x)*(p2.x - p1.x) + (p2.y - p1.y)*(p2.y -p1.y));
}
};
//==================================================================================
//vector segment or line
//==================================================================================
class Vector
{
public:
Point start;
Point end;
double _x;
double _y;
double a,b,c; //ax + by + c = 0
Vector(){}
Vector(double __x,double __y):_x(__x),_y(__y){}
Vector(Point a,Point b):start(a),end(b) { _x = end.x - start.x; _y = end.y - start.y; }
//operator
//judge the position of the point relative to the segment
double operator*(const Point& _P)const
{
double res = Point::crossProduct(_P,this->end,this->start);
if(fabs(res) < EPS)
return 0;
if(res > 0)
return 1;
else
return -1;
}
//crossProduct
double operator*(const Vector& _V)const
{
Point st = _V.start;
Point en = _V.end;
return Point::crossProduct(start,end,st,en);
}
//transfer to normal rex
bool pton()
{
a = start.y - end.y;
b = end.x - start.x;
c = start.x * end.y - start.y * end.x;
return true;
}
//judge whether _P is on the line
bool IsLinehasPoint(const Point& _P)const
{
if(fabs((*this)*_P) < EPS)
return true;
else
return false;
}
//juegde whether _P is on the segment
bool IsSegmenthasPoint(const Point& _P)const
{
if(_P.x >= min(this->start.x,this->end.x) && _P.x <= max(this->start.x,this->end.x) &&
_P.y >= min(this->start.y,this->end.y) && _P.y <= max(this->start.y,this->end.y) &&
fabs((*this)*_P) < EPS
)
return true;
else
return false;
}
//the distance from point to line
double disToPoint(const Point& _P)
{
pton(); //transfer
double td = (a*_P.x + b*_P.y + c)/sqrt(a*a + b*b);
double xp = (b*b*_P.x - a*b*_P.y -a*c)/(a*a + b*b);
double yp = (-a*b*_P.x + a*a*_P.y - b*c)/(a*a + b*b);
double xb = max(start.x,end.x);
double yb = max(start.y,end.y);
double xs = start.x + end.x - xb;
double ys = start.y + end.y - yb;
if(xp > xb + EPS||xp < xs - EPS||yp > yb + EPS||yp < ys - EPS)
td = min(_P.dis(start),_P.dis(end));
return fabs(td);
}
//out the mirror point by this line or segment
Point mirrorPoint(const Point& _P)const
{
Point ret;
double d = a * a + b * b;
ret.x = (b*b*_P.x - a*a*_P.x - 2*a*b*_P.y - 2*a*c)/d;
ret.y = (a*a*_P.y - b*b*_P.y - 2*a*b*_P.x - 2*b*c)/d;
return ret;
}
//out the vertical line of two points
static Vector verticalLine(const Point& _a,const Point& _b)
{
Vector ret;
ret.start.x = (_a.x + _b.x)/2;
ret.start.y = (_a.y + _b.y)/2;
ret.a = _b.x - _a.x;
ret.b = _b.y - _a.y;
ret.c = (_a.y - _b.y)*ret.start.y + (_a.x - _b.x)*ret.start.x;
if(fabs(ret.a) > EPS)
{
ret.end.y = 0.0;
ret.end.x = -ret.c/ret.a;
if(ret.end == ret.start)
{
ret.end.y = 1e10;
ret.end.x = -(ret.c - ret.b * ret.end.y)/ret.a;
}
}
else
{
ret.end.x = 0.0;
ret.en补充:软件开发 , C++ ,