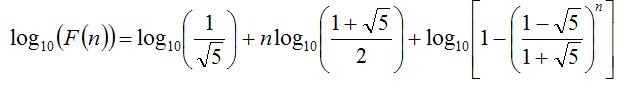c++常见的算法快速分析解决(二)
题目:斐波那契数列,FIBONACCI数列特点是第1,第2两个数为1,1.从第3个数开始,该数是前两个数之和,求这个数列的前30个元素
分析: 費波那西數列(Fibonacci Sequence),又譯費波拿契數、斐波那契數列、費氏數列、黃金分割數列。在數學上,費波那西數列是以遞歸的方法來定義:
F0 = 0
F1 = 1
Fn = Fn- 1 + Fn - 2
用文字來說,就是費波那西數列由 0 和 1 開始,之後的費波那西係數就由之前的兩數相加。首幾個費波那西係數是(OEIS A000045):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,
4181, 6765, 10946,………………
特別指出:0不是第一項,而是第零項。(参考)
分析题目我们可以用如下等式来表示斐波那契数列:
F1=1----(n=1);
F2=1----(n=1);
Fn=F(n-1)+F(n-2)-----(n>=3)
这里我们将F的下标看成是数组的下标代码如下:
#include<stdio.h>#include<stdlib.h>int main(){ int i;/*定义整形变量*/ long f[31];/*定义数组为长整形*/ f[1]=f[2]=1;/*数组的f[1],f[2]赋值为1*/ for(int i=3;i<31;i++) { f[i]=f[i-1]+f[i-2];/*数组从第三行开始,每一项等于前两项之和*/ } for(i=1;i<31;i++) { printf("%10ld",f[i]);/*输出数组中的30个元素*/ if(i%5==0) printf(" ");/*每5个元素进行一次换行*/ } system("PAUSE"); }结果:
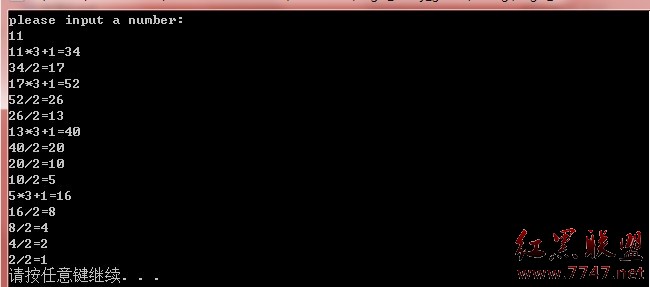
题目:角谷猜想 ,任意一个自然数,当他为偶数的时候则除以2,当他为奇数的时候则乘3加1,得到一个新的自然数,依次按照这个法则继续演算,到很多次以后,就会得到一个结果,这个结果是1...
分析:考拉兹猜想,又称为3n+1猜想、冰雹猜想、角谷猜想、哈塞猜想、乌拉姆猜想或叙拉古猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1,如果它是偶数,则对它除以2,如此循环,最终都能够得到1。(易做图)
有题目分析可知,重点是判断一个数是奇数还是偶数,程序采用对2取余的方法,当余数为0时,说明该数为偶数,否则为奇数
举例:取一个数字如n = 6,根据上述数式,得出 6→3→10→5→16→8→4→2→1 。(步驟中最高的數是16,共有7個步驟)
如n = 11,根据上述数式,得出 11→34→17→52→26→13→40→20→10→5→16→8→4→2→1。(步驟中最高的數是40,共有13個步驟)
如n = 27,根据上述数式,得出 : 27→82→41→124→62→31→94→47→142→71→214→107→322→161→484→242→121→364→182→91→274→137→412→206→103→310→155→466→233
→700→350→175→526→263→790→395→1186→593→1780→890→445→1336→668→334→167→502→251→754→377→1132→566→283→850→425→1276
→638→319→958→479→1438→719→2158→1079→3238→1619→4858→2429→7288→3644→1822→911→2734→1367→4102→2051→6154→3077→9232
→4616→2308→1154→577→1732→866→433→1300→650→325→976→488→244→122→61→184→92→46→23→70→35→106→53→160→80→40→20→10
→5→16→8→4→2→1。(步驟中最高的數是9232,共有111個步驟)
考拉兹猜想称,任何正整数,经过上述计算步骤後,最终都会得到 1 。代码:
#include<stdio.h>#include<stdlib.h>void main(){ long i,n; //定义变量为长整形 printf("please input a number: ");//输入任意一个长整形数 scanf("%ld",&n); while(n!=1) { if(n%2==0) //判断是否为偶数 { printf("%ld/2=%ld ",n,n/2);//当为偶数的时候n除以2 n=n/2; } else { printf("%ld*3+1=%ld ",n,n*3+1);//当我奇数时乘以3加1 n=n*3+1; } } system("pause");}结果:
题目:歌德易做图猜想,验证100以内的的正偶数都能分解为两个素数之和
分析:任一大於2的偶數,都可表示成兩個質數之和。
將一給定的偶數表示成兩個質數之和被稱之為此數的哥德易做图分割。例如,
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
…
換句話說,哥德易做图猜想主張每個大於等於4的偶數都是哥德易做图數-可表示成兩個質數之和的數[1]。哥德易做图猜想也是希爾伯特第八問題中的一個子問題。
另有對奇數的相似猜想,稱之為勒穆瓦纳猜想(Lemoines conjecture)或李維猜想(Levys conjecture)。
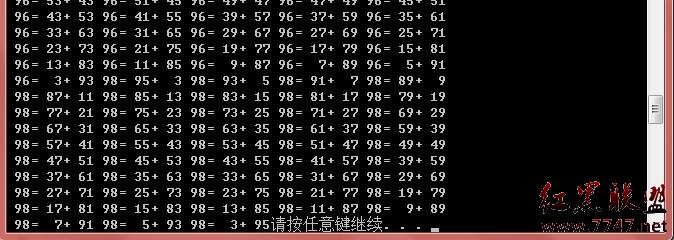
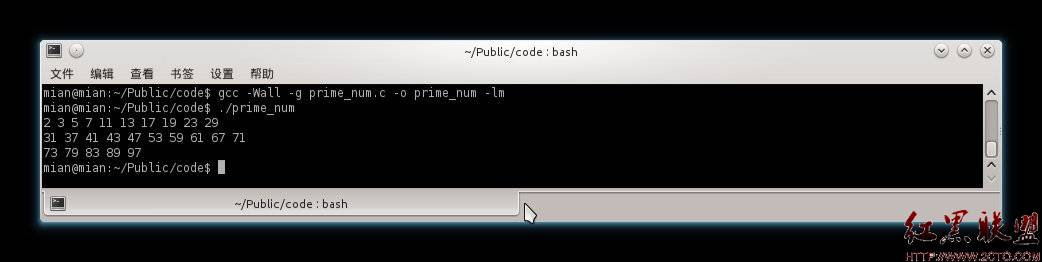
为了验证哥德易做图猜想对100以内的正偶数成立,所以要将正偶数分为两部分,在对这两部分进行判断,如果均是素数则满足体艺,不是的话,则重新分解继续判断代码:
#include<stdio.h>#include<stdlib.h> int ss(int i)/*自定义一个函数是不是素数*/ { int j; if(i<=1)/*小于1的不是素数*/ return 0; if(i==2) /*2是素数*/ return 1; for(j=2;j<i;j++)/*对大于2的进行判断*/ { if(i%j==0) return 0; else if(i!=j+1) return 1; } } void main() { int i,j,k,flag1,flag2,n=0; for(i=6;i<100;i+=2) for(k=2;k<=i;k++) { j=i-k; flag1=ss(k); if(flag1) /*判断拆分的数是不是素数*/ { flag2=ss(j); if(flag2) /*如果拆分出来的数是素数则输出*/ { printf("%3d=%3d+%3d",i,j,k); n++; if(n%5==0) printf(" "); } } } system("pause"); } 结果:
题目:四方定理,所有的自然数至多只要4个数的平方和就可以表示,编程验证
可以采用穷举试探的方法进行计算,当满足定理的条件就可以输出结果
代码:
#include<stdio.h>#include<stdlib.h>int main(){ long i,j,k,l,n;//定义变量为长整形 printf("请输入 一个长整形的整数"); scanf("%ld",&n); for(i=0;i<n;i++) //对i,j,k,l进行穷举 for(j=0;j<i;j++) for(k=0;k<j;k++)
补充:软件开发 , C++ ,