hdu-4607-Park Visit

Problem Description
Claire and her little friend, ykwd, are travelling in Shevchenko's Park! The park is beautiful - but large, indeed. N feature spots in the park are connected by exactly (N-1) undirected paths, and Claire is too tired to visit all of them. After consideration, she decides to visit only K spots among them. She takes out a map of the park, and luckily, finds that there're entrances at each feature spot! Claire wants to choose an entrance, and find a way of visit to minimize the distance she has to walk. For convenience, we can assume the length of all paths are 1.
Claire is too tired. Can you help her?

解析：类似于找一个最长的树根，即
*__*__*__*__*__*__*__*__*__
          |         |    |    |
          *        *    *    *
          |         |
          *        *

其次就是找最长的树根时，要两次遍历：

1. 第一次遍以任意一个点A出发，找到距离最远的那个点B。

2. 再从B出发，找到距离B最远的那个点C，则BC线段长度即为树根长。

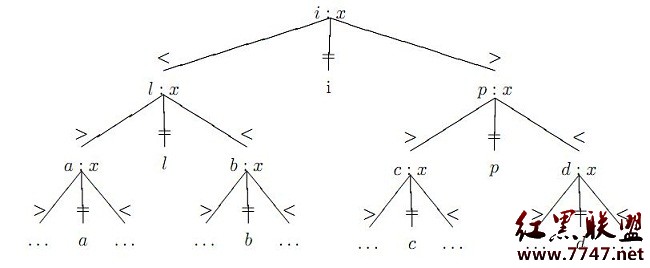
证明：首先，B 一定是直径的一端。

a) 如果 A 是直径的一端，那么 B 显然是直径的另一端，结论成立。

b) 如果 A 不是直径的一端，那么路径（A->B）一定与直径交于一点 p，且（p->B）一定是直径的一部分，推出 B 是直径的一端，结论成立。

1> 为什么一定存在交点 p?

如果不存在交点 p ，由于树是连通的，那么加若干边使得直径经过（A->B）上的一点 p，直径不会变得更短。

2>为什么（p->B）一定是直径的一部分。

如果不是，（A->B）就不是从 A 到 B 最长的路径。

然后大家就明白了，设树根长为L，假如要参观的景点N<=L，则输出 N-1 ，否则，输出 L - 1 + 2 * ( N - L )。
具体代码如下：

#include<string.h>   
#include<vector>   
#include<queue>   
using namespace std;  
int s[100005];  
int main()  
{  
    int N,m,n,a,b,i,l;  
    scanf("%d",&N);  
    while(N--)  
    {  
        scanf("%d%d",&m,&n);  
        vector<int> Q[100005];  
        queue<int> q;  
        memset(s,0,sizeof(s));  
        for(i=0;i<m-1;i++)  
        {  
            scanf("%d%d",&a,&b);  
            Q[a].push_back(b);  
            Q[b].push_back(a);  
        }  
        q.push(1);s[1]=1;  
        while(!q.empty())  
        {  
            a=q.front();  
            for(i=0;i<Q[a].size();i++)  
            {  
                if(!s[Q[a][i]])  q.push(Q[a][i]);  
            }  
            s[a]=1;q.pop();  
        }  
        q.push(a);memset(s,0,sizeof(s));s[a]=1;  
        while(!q.empty())  
        {  
            a=q.front();  
            for(i=0;i<Q[a].size();i++)  
            {  
                if(!s[Q[a][i]])  {q.push(Q[a][i]);s[Q[a][i]]=s[a]+1;}  
            }  
            q.pop();  
        }  
        l=s[a];  
        while(n--)  
        {  
            scanf("%d",&a);  
            if(a<=l) printf("%d\n",a-1);  
            else     printf("%d\n",l-1+2*(a-l));  
        }  
    }  
}

补充：软件开发 , C++ ,