(step6.3.4)hdu 1151(Air Raid——最小路径覆盖)

题意：

一个镇里所有的路都是单向路且不会组成回路。

派一些伞兵去那个镇里，要到达所有的路口，有一些或者没有伞兵可以不去那些路口，只要其他人能完成这个任务。每个在一个路口着陆了的伞兵可以沿着街去到其他路口。我们的任务是求出去执行任务的伞兵最少可以是多少个。

思路：

这个题就是个最小路径覆盖问题。

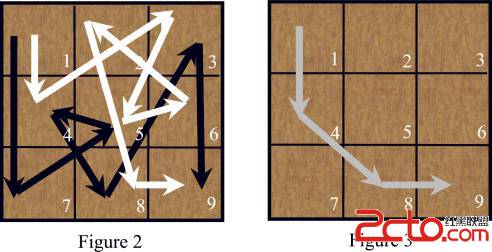
路径覆盖的定义是：在有向图中找一些路径，使之覆盖了图中的所有顶点，就是任意一个顶点都跟那些路径中的某一条相关联，且任何一个顶点有且只有一条路径与之关联，一个单独的顶点是一条路径.最小路径覆盖就是最少的路径覆盖数。

如上图，最小路径覆盖的那条路应该是{e1,e4,e5,e6,e7},最小路径覆盖就是1。

有定理：最小路径覆盖 = 图的顶点数 – 最大匹配数。

其实那个最大匹配数并非原图的最大匹配数，而是最小路径覆盖的边的条数，是把图中每个点拆成两个点，再算出来的最大匹配数。很容易证明两者是相同的。

可是有一点不明白，为什么原图用匈牙利算法算出最大匹配数，与图的顶点数想减，最后求出的最小路径覆盖是对的呢，而不需要用拆点后的图来算呢？

-----原来我建的邻接表它本身就拆点了，所以不矛盾。

--------------------------以上为摘抄别的大牛的

代码如下:

/* 
 * 1151_1.cpp 
 * 
 *  Created on: 2013年8月31日 
 *      Author: Administrator 
 */  
#include <iostream>  
  
using namespace std;  
  
const int maxn = 1001;  
int map[maxn][maxn];  
int link[maxn];  
bool useif[maxn];  
int n;  
  
int can(int t){  
    int i;  
    for(i = 1 ; i<= n ; ++i){  
        if(useif[i] == 0 && map[t][i]){  
            useif[i] = 1;  
            if(link[i] == - 1 || can(link[i])){  
                link[i] = t;  
                return 1;  
            }  
        }  
    }  
  
    return 0;  
}  
  
int max_match(){  
    int i;  
    int num = 0;  
    memset(link,-1,sizeof(link));  
    for(i = 1 ; i <= n ; ++i){  
        memset(useif,0,sizeof(useif));  
        if(can(i)){  
            num++;  
        }  
    }  
    return num;  
}  
  
int main(){  
    int t;  
    scanf("%d",&t);  
    while(t--){  
        int k;  
        memset(map,0,sizeof(map));  
        scanf("%d%d",&n,&k);  
  
        int i;  
        for(i = 1 ; i <= k ; ++i){  
            int a,b;  
            scanf("%d%d",&a,&b);  
            map[a][b] = 1;  
        }  
  
        printf("%d\n",n - max_match());  
  
    }  
}

补充：软件开发 , C++ ,