算法导论Problem6-3 Youngtableau问题 堆排序应用

其实这也是应用堆排序的思想，就是把这个数组的看做是二叉树组成的。一个元素的下面一行的对应一个元素是它的左孩子，右边一个元素是它的右孩子。

这样就可以应用堆排序来解决这个问题了。

同时也是像堆排序一样，实际使用一维数组存储数据，人为规定（按照堆排序的规则，这个是关键思维）地构造二维数组来存储二叉树。

详细程序如下：

 

#include<iostream>  
#include<vector>  
  
using namespace std;  
  
int gChildren = 2;  
int column = 4;  
//实际用以为数组表示数据，但是通过人为地规定，构造了一个二维数组，同理可以很轻松地构造三维数组  
  
//主要不同之处就是寻找孩子和父母节点不一样了  
int youngTableauUpParent(int cIndex)    //cIndex 为C下标0开始  
{  
    return cIndex-column;  
}  
  
int youngTableauleftParent(int cIndex)  
{  
    return cIndex-1;  
}  
  
int youngTableauChild(int cIndex, int leftOrRight)  //cIndex 为C下标0开始  
{  
    if(leftOrRight==1)//代表左孩子  
        return cIndex+column;  
    else //代表是右孩子  
        return cIndex+1;  
}  
  
//找出当前节点和其孩子们的当中的最大值;  
//本人觉得是本人创造的非常妙的从youngTableauify函数中分离出来的功能函数。极大的简化了对本算法的理解。  
template<typename T>  
int youngTableauMax(vector<T>& youngTableau, int cIndex, int youngTableauSize)  
{  
    T tempMax = youngTableau[cIndex];  
    int childIndex = 0;  
    int tempIndex = cIndex;  
    //不同处：如果是最右一列就没有右孩子，如果是最下面一行就没有左孩子，就直接跳过  
    if(youngTableauChild(cIndex, 1)<youngTableauSize)   
    {  
        childIndex = youngTableauChild(cIndex, 1);//1代表左孩子  
        if(youngTableau[childIndex]>tempMax)  
        {  
            tempMax = youngTableau[childIndex];  
            tempIndex = childIndex;  
        }  
    }  
    //注意：少了第二个判断条件会出现错误结果，而且很难Debug。千万不能漏了条件  
    if((cIndex+1)%column!=0 && (cIndex+1)<youngTableauSize)  
    {  
        childIndex = youngTableauChild(cIndex, 2);//2代表右孩子  
        if(youngTableau[childIndex]>tempMax)  
        {  
            tempMax = youngTableau[childIndex];  
            tempIndex = childIndex;  
        }  
    }  
    return tempIndex;  
}  
  
//与堆排序一模一样  
//We assume cIndex's children have all been youngTableauified, which is the key to make this algorithm work!!!  
//比之前的二叉树堆排序更加简洁明了点  
template<typename T>  
void youngTableauify(vector<T>& youngTableau, int cIndex, int youngTableauSize)  
{  
    if(cIndex<youngTableauSize)  
    {  
        int tempIndex = youngTableauMax(youngTableau, cIndex, youngTableauSize);  
        if(tempIndex != cIndex)  
        {  
            swap(youngTableau[cIndex], youngTableau[tempIndex]);  
            youngTableauify(youngTableau, tempIndex, youngTableauSize);   
        }  
    }  
}  
  
template<typename T>  
void buildMaxyoungTableau(vector<T>& youngTableau)  
{  
    for(int i=(youngTableau.size()-1); i>=0; i--)    //不同处：从下表倒数第二个开始  
        youngTableauify(youngTableau, i, youngTableau.size());  
}  
  
//与堆排序一模一样  
template<typename T>  
void youngTableauSort(vector<T>& youngTableau)  
{  
    buildMaxyoungTableau(youngTableau);  
    for(int i=youngTableau.size()-1; i>0; i--)  
    {  
        swap(youngTableau[0], youngTableau[i]);  
        youngTableauify(youngTableau, 0, i);  
    }  
}  
  
template<typename T>  
void youngTableauPrint(const vector<T>& youngTableau)  
{  
    int i = 1;  
    for(auto x:youngTableau)  
    {  
        cout<<x<<"\t";  
        if(i%column==0) cout<<endl;  
        i++;  
        //输出格式化的数组，方便检查  
    }  
    cout<<endl;  
}  
  
  
void test()  
{  
    //初始化数组  
    int a[15] = {2,4,7,1,4,8,9,31,83,28,48,94,87,16,36};  
    vector<int> youngTableau(a, a+15);  
  
    //序列输出  
    cout<<"Befor build youngTableau:\n";  
    youngTableauPrint(youngTableau);  
  
    //建立大顶堆后输出  
    cout<<"After build youngTableau:\n";  
    buildMaxyoungTableau(youngTableau);  
    youngTableauPrint(youngTableau);  
  
    //排序后  
    cout<<"After sort:\n";  
    youngTableauSort(youngTableau);  
    youngTableauPrint(youngTableau);  
}  
  
int main()  
{  
    test();  
    return 0;  
}  

 

 

结果：

可以改变column，以改变列数，来看看结果如何，而且最后一行可以是不满列，列如本例中column等于4的时候：

column = 3:

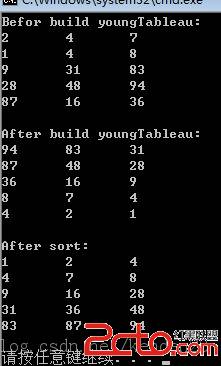
column = 4:

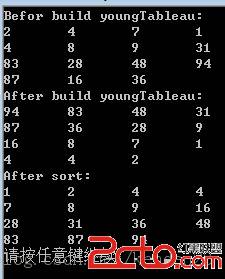
可以是任意列数，甚至可以是column=1，column=100，会有有趣的结果哦，呵呵。有兴趣的可以试一试，想想为什么。

补充：软件开发 , C++ ,