动态规划之多边形游戏

 

依次编号为1~N。下图给出了一个N＝4个顶点的多边形。

 

 

  

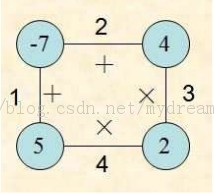
 游戏规则 ：(1) 首先，移走一条边。 (2) 然后进行下面的操作： 选中一条边E，该边有两个相邻的顶点，不妨称为V1和V2。对V1和V2顶点所标的整数按照E上所标运算符号(+或是×)进行运算，得到一个整数；用该整数标注一个新顶点，该顶点代替V1和V2 。 持续进行此操作，直到最后没有边存在，即只剩下一个顶点。该顶点的整数称为此次游戏的得分(Score)。

 

解决思想我就不多介绍了，网上很多资料。下面我贴下我看完资料后的实现。

 

 

 

 

/* 
    经典动态规划应用 
    m[i][j][0],m[i][j][1]分别为从第i个节点开始的j个节点所能求的最小值和最大值，只要我们找到了i从1-<span style="white-space:pre">  </span>-N时j为N的m集合也就找到了整个 
    游戏的最大值m[i][N][1]。 
    那么怎么求m[i][j][0],m[i][j][1],这就要用到动态规划。 
    m[i][j][0],m[i][j][1]的节点和边集合T为：节点i，边i+1，节点i+1,边i+2.......边i+j-1,节点i+j-1。 
    能求出m[i][j][1]，那么必须比较在边i+1,i+2,....i+j-2,i+j-1（他们把T集合分成了两个小集合T1,T2）<span style="white-space:pre">    </span>合并边的时能求的大小。 
    这里有点开始像分治的思想了。 
*/  
#include<iostream>  
using namespace std;  
  
#define MAX 1024  
char op[MAX];//记录边的符号+ , *  
int m[MAX][MAX][2];//记录m[i][j][0],m[i][j][1]  
int N;  
  
void dealFunc(int n,int i,int j)//处理从第i节点开始的连续j个节点，求出m[i][j][0],m[i][j][1]  
{  
    for(int k=1;k<=j-1;k++)  
    {  
        int a=m[i][k][0];  
        int b=m[i][k][1];  
        int next=i+k;  
        if(next>N)//边界问题  
            next%=N;  
        int c=m[next][j-k][0];  
        int d=m[next][j-k][1];  
        int max,min;  
        if(op[next]=='+')//+  
        {  
            max=b+d;  
            min=a+c;  
        }  
        else//* 这里就是为什么还要求m[i][j][0]的原因啦。  
        {  
            int e[4];  
            e[0]=a*c;  
            e[1]=a*d;  
            e[2]=b*d;  
            e[3]=b*c;  
            min=e[0];  
            max=e[0];  
            for(int i=1;i<4;i++)  
            {  
                if(min>e[i])  
                    min=e[i];  
                if(max<e[i])  
                    max=e[i];  
            }  
  
        }  
  
        if(m[i][j][0]>min)  
            m[i][j][0]=min;  
        if(m[i][j][1]<max)  
            m[i][j][1]=max;  
    }  
}  
  
void main()  
{  
    cout<<"请输入点的个数:";  
    cin>>N;  
    int i,j;  
    int value;  
    char edgeFlag;  
    //整个游戏节点和边集合顺序为边1,节点1,边2,节点2.......边N,节点N  
    for(i=1;i<=N;i++)  
    {  
        cout<<"请输入点和边的值";  
        cin>>edgeFlag>>value;  
        m[i][1][0]=m[i][1][1]=value;  
        for(j=2;j<=N;j++)  
        {  
            m[i][j][0]=MAX;  
            m[i][j][1]=MAX*(-1);  
        }  
        op[i]=edgeFlag;  
    }  
    for(j=2;j<=N;j++)  
    {  
        for(int i=1;i<=N;i++)  
        {  
            dealFunc(N,i,j);  
        }  
    }  
      
    int max=m[1][N][1];  
    int edge=1;  
    for(i=1;i<=N;i++)  
    {  
        cout<<"删除第"<<i<<"条边时为 "<<m[i][N][1]<<endl;  
        if(m[i][N][1]>max)  
        {  
            max=m[i][N][1];  
            edge=i;  
        }  
    }  
    cout<<"删除第"<<edge<<"时为最大:"<<max<<endl;  
}  

 

补充：软件开发 , C++ ,