算法学习之数据结构之叉查找树
一,先介绍一些二叉查找树的概念和性质。
二叉树执行基本操作的时间与树的高度成正比。
设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]。
注意这个性质,这个性质表示二叉查找树的根节点的左子树中所有结点都小于根结点,所有右子树的结点都大于根结点。所以根据这个性质,可以用中序访问二叉查找数来实现从小大到排列。
二叉查找树的几个操作:
SEARCH:查找关键字等于key的结点
MINIMUM:找出关键字最小的结点
MAXIMUM:找出关键字最大的结点
SUCCESSOR:找出结点x的后继y
INSERT:在二叉查找树中插入结点z
DELETE:在二叉查找树中删除结点z
里面就INSERT和DELETE麻烦一些。
二、下面分别用伪代码实现上述操作。
中序遍历
[plain]
inorder-tree-walk(x)
if x != null
then inorder-tree-walk(left[x])
print(x)
inorder-tree-walk(right[x])
查找
[plain]
tree-search(x, k)
if x == null or k = key[x]
then return x;
if k < key[x]
then return tree-search(left[x], k)
else return tree-search(right[x], k)
时间是树的高度h=logn
while版本,不用递归
while x!= null and k != key[x]
do if(k < key[x])
then x = left[x]
else x = right[x]
return x
最小元素的指针(左子树的左节点)
[plain]
tree-minimum(x)
while left[x] != null
do x = left[x]
return x
后继
[plain]
tree-successor(x)
1 if right[x] != null //如果x有右子树,则在右子树中寻找最小值
2 then return tree-minimum(right[x])
3 y = parent[x]
4 while y !=null and x == right[y] //如果没有右子树,则其后继y,是x的父亲结点的第一个右子树
5 do x == y
6 y == parent[y]
7 return y
根据其后继的特性,结点x的后继是具有大于key[x]中的关键字最小者的那个结点。
第1~2行,x的右子树的结点都是大于key[x]的结点,所以如果x有右子树,则在右子树中寻找最小值
第3~6行,如果没有右子树,则其后继y,是x的父亲结点的第一个右子树(根据后继的特性:结点x的后继是具有大于key[x]中的关键字最小者的那个结点。因为x没有右子树,所以这时,按中序遍历的x下一个结点即后继,应该是这样一个子树的根结点y,x的祖先是其左孩子,这样,y就大于其左子树所有结点,并且因为x是y的左子树中最大的结点了)。
插入:
把结点z插入二叉查找数T中,分以下几步:
1.将key[z]从根结点x开始比较,并用y记录x的父亲结点,直到到达最后一层某一叶节点比较完,此时y指向某一叶节点,x是NULL。
2.如果此时y是NULL,则证明是空树,于是根结点就是z
3.否则如果key[z]小于key[y],则让left[y] = z;当key[z]大于或等于key[y],则让right[y] = z。
具体为代码如下:
[plain]
tree-insert(T, z)
y = null
x = root[T]
while x != null
do y = x
if(key[x] < key[z])
then x = right[x]
else x = left[x]
parent[z] = y
if(y == null) //树是空的
then root[T] = z
else if key[z] < key[y]
then left[y] = z
else right[y] = z
删除:
有三种情况:
1,没有左子树和右子树。这个就是直接删除z,把z的父亲结点parent[z]指向z的子树设置为NULL。、
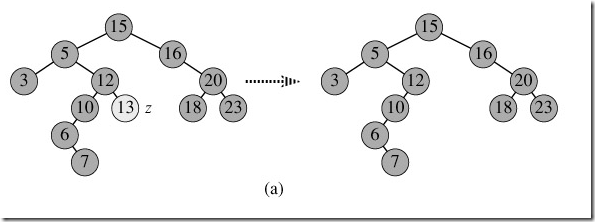
2,只有左子树或者只有右子树。这个是让z的子树与其父亲结点相连,删除z即可。
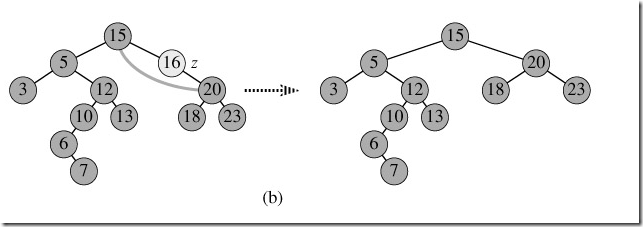
3,既有左子树又有右子树。这是先用succeor方法找到要删除节点z的后继y,因为y一定没有左子树(因为y是z的后继,参看上文关于后继的定义,所以y是z的右子树中最小的一个结点,如果y还有左子树,则y的左子树中的结点一定比y小!),所以可以删除y,并让y的父亲结点成为y的右子树的父亲结点(类似第2中情况),并用y的key代替z的key。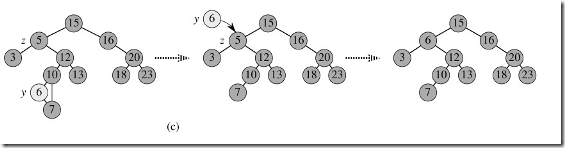

具体伪代码如下:
[plain]
tree-delete(T, z)
if left[z] == null or right[z] == null //如果没有做孩子节点或者没有右孩子节点,及至多有一个子树
then y = z
else y = tree-successor(z) // 如果都有左孩子和右孩子,则找到他的后继节点
if left[y] != null
then x = left[y]
else x = right[y]
if x != null // 如果只有一个孩子节点
then parent[x] = parent[y] //让z的子树x与其父亲结点相连,删除z即可。
if parent[y] == null //如果y没有父亲节点,说明是根节点
then root[T] = x //则使它的孩子节点为父亲节点
else if y == left[parent[y]] //如果y是其父亲节点的左子树,所以可以删除y,并让y的父亲结点成为y的右子树的父亲结点
then left[parent[y]] = x
else right[parent[y]] = x
if y != z
then key[z] = key[y] //并用y的key代替z的key。
return y
补充:软件开发 , C语言 ,