约瑟夫问题的N种解法


		有n个囚犯站成一个圆圈，准备处决。首先从一个人开始报数,报到k的人被处死,剩下n-1个人继续这个过程,直到最终只剩下一个人留下.
 
问题是，给定了n和k，一开始要站在什么地方才能避免被处决？
 
 
 
 模拟实现
 
 
 
我们利用计算机来模拟这个过程,可以得到最后的结果.
 
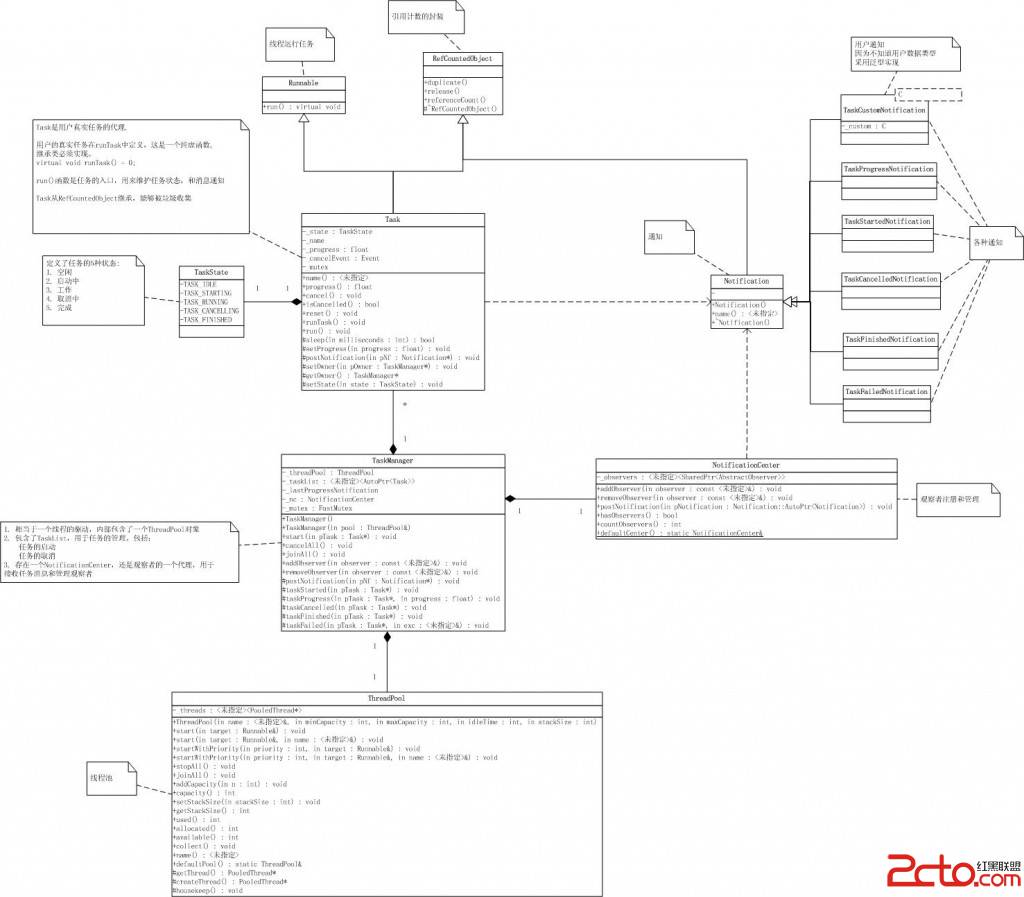
具体的编码中,考虑到每次要随机删除一个人,用链表实现比较方便.然后又是一个圈,可以考虑用循环链表.
 
指针从头到尾遍历到k,删去节点,直到只剩下一个节点为止.
 
简单的编码如下:
 
[cpp]  
#include<iostream>  
using namespace std;  
int *A;  
int f(int n,int k)  
{  
    int p=1;int q=n;  
    int count=n;  
    while(count--)  
    {  
        for(int i=0;i<k-1;i++)  
        {  
            q=p;  
            p=A[p];  
        }  
        A[q]=A[p];  
        p=A[p];  
    }  
    return p;  
}  
int main()  
{  
    int n,k;  
    cin>>n>>k;  
    A=new int[n+1];  
    for(int i=1;i<n;i++)  
    {  
        A[i]=i+1;  
    }A[n]=1;  
    cout<<f(n,k)<<endl;  
    return 0;  
}  
 
 数学解法
 
 
 
因为k==2的时候有较多的研究,也有较直观和简单,简单到位级别的算法,我们先来考虑k==2的情况.
 
 
 
当k==2时,所有的偶数哥死掉了.剩下基数们,重新排列后,原来位置是x的哥,排到了(x+1)/2的位置(有兴趣的可以自己画画图).
 
用函数f(n)表示,当序列还有n个人的时候幸存者的位置.如下图：
 
 

 
根据上面的说法,可以得出下面公式:
 
 
 
N为偶数:f(N)=2*f(N/2)+1;
 
N为基数:f(N)=2*f((N-1)/2)+1;                                                                                       (1)
 
幸存者一直活到N=1的时候,即
 
f(1)=1;                                                                                                                           (2)
 
根据上面(1)(2),我们可以写出简单的递推方法,
 
F (1) = 1;
 
f (2n) = 2f (n) - 1; 当 n>1;
 
f (2n + 1) = 2f (n) + 1; 当 n>1;
 
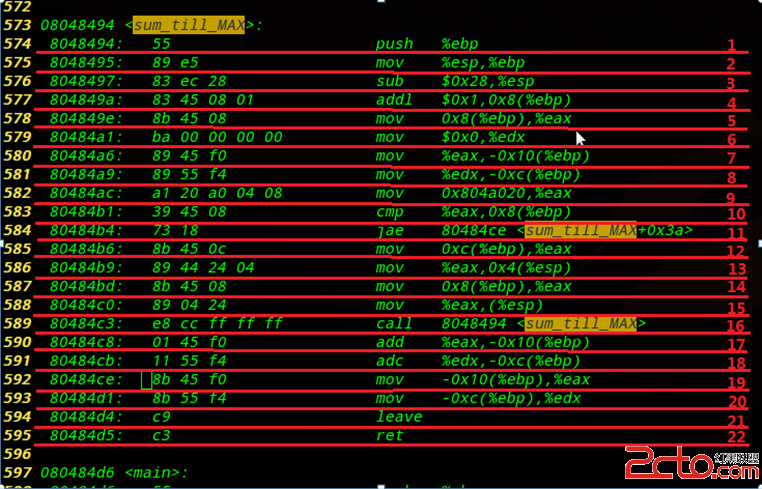
从1->N递推,时间复杂度为O(N);
 
[cpp] 
A[1]=1;  
int f(int n)  
{  
    for(int i=2;i<=n;i++)  
        A[i]=i&1?((A[i>>1]<<1)+1):(((A[i>>1])<<1)-1);  
    return A[n];  
}  
 
或者用递归函数,从N->1,时间复杂度为O(logN).
 
[cpp]  
int f(int n)  
{  
    if(!(n^1))  
        return 1;  
    if(n&1)  
        return 2*f((n-1)/2)+1;  
    else  
        return 2*f(n/2)-1;  
}  
 
接着我们要推出更简洁的方法.
 
列出的f(N)与N如下:
 
N     1,    2     3     4,    5     6     7     8,    9     10    11    12    13    14    15    16,
 
F(N)1     1     3     1     3     5     7     1     3     5     7     9     11    13    15    1
 
通过观察我们能够发现,f(N)是一个基数的循环,以2^m为开头,即:
 
如果N=2^m+L,(0<=L<2^m),那么f(N)=2*L+1;
 
 
当然,看到2^m,我们很自然地想到要用位操作解决.
 
2^m,即m+1位为1;如2^3=8的二进制数就是1000.
 
N 的二进制表示为:N=b0b1b2b3….,其中b0表示非0的最高位.
 
那么2^m<N的最大2^m为b0,000000,(N-2^m)*2+1=b1b2…..b0.
 
 
 
也就是f(b0b1b2..)=b1b2..b0;
 
OK,开始编码:
 
[cpp]  
int f(int n)  
{  
    int pos=1;int temp=1;  
    for(int i=0;i<31;i++)  
    {  
        if(n&pos)  
            temp=pos;  
        pos=(pos<<1);  
    }  
    return ((n-temp)<<1)+1;  
}

补充：软件开发 , C++ ,