数据结构之链表与数组（三）－单向链表上的简单操作

思路：

图1  非递归反转链表

      如图1所示，假设已经反转了前面的若干节点，且前一段链表的头节点指针为pre，则现在要做的事情是首先保存当前节点cur后面的链表，然后让当前节点cur的指针与后面的节点断开(step1)，接下来再将当前节点的next指针指向前一段链表的头节点pre (step2)。处理完当前节点的连接反转后，所有的指针都向后移一位。开始处理下一个节点。

      注意点：

      1，反转后原来的头节点就变成了反转链表的尾节点，要注意将此结点next指针设为空，否则可能会产生死循环等问题

      2，要记得处理链表中没有节点或只有一个的情况。

代码实现：

//反转链表（非递归的方式）
//输入参数：单链表的头指针
//输出参数：无
//返回值：反转后的单链表指针
SingleList* Reverse_NRecu(SingleList *head)
{
	SingleList *pre,*cur,*lat;

	//链表中没有节点或只有一个节点
	if((head == NULL)||(head->next == NULL))
	{
		return head;
	}

	pre = head;
	cur = head->next;
	head->next = NULL;//在链表中应该注意边界情况的处理，尾结点一定要为空
	lat = cur->next;

	while(lat != NULL)
	{
		cur->next = pre;
		pre = cur;
		cur = lat;
		lat = lat->next;
	}
	cur->next = pre;
	return cur;
}

5  反转单向链表（递归实现）

思路：

      在用递归实现问题时，要时刻注意在分析时我们只要重点分析第一层和第二层之间的关系就可以了，不要随着递归一直向下思考。如果考虑的层次太多，可能会陷入进行而越想越乱。递归中另一个要特别注意的是，递归的终止条件。一定要把什么时候结束、怎么结束想清楚。

对于链表的反转：

图2  递归实现反转链表

      考虑第一层和第二层之间的关系时，我们假定第二层后面的链表已经处理完毕了，它返回了后面链表的尾指针，如图2所示（蓝色框包含的节点是后继要递归的节点，在考虑第一层时我们假定它们已经反转成功了）。这时我们只要将返回的指针cur的next指向当前指针，就完成了当前节点的反转。反转后新加入反转链的指针pre返回即可。

      另一个要考虑的就是递归的终止条件，问题的终止是当递归到最后一个节点时，它后面已经没有节点，这是直接返回这可以了。

代码实现：

//反转链表（递归的方式）
//输入参数：单链表的头指针
//输出参数：反转链表后的新的指针
//返回值：反转后单链表的最后一个指针
SingleList* Reverse_Recu(SingleList *head,SingleList **newHead)
{
	SingleList *pSL;

	//终止条件
	if((head == NULL)||(head->next == NULL))
	{
		*newHead = head;
		 return head;
	}

	pSL = Reverse_Recu(head->next,newHead);
	pSL->next = head;
	head->next = NULL;
	return head;
}

6  判断单向链表是否有环

思路：

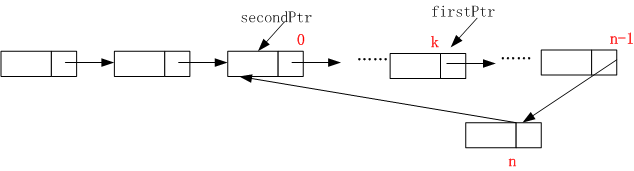
图3  带环的单向链表

      一般看到这个问题，我们都能想到简单方法可能是，逐个节点地遍历链表，并记录遍历过节点的地址，在遍历下一个节点时判断其是否在已经遍历过的节点集合中，如果在则说明链表有环。这种方法的时间复杂度是O（n²）。

      我在网上查到一个更高效的方法。它与前面第3题的方法类似，设置两个遍历指针，第一个指针firstPtr每次走两步，第二个指针每次走一步，这样如果两个指针能相遇则说明链表有环。

      分析可得，如果链表有环，则在第二个指针第一次到达环的入口节点时，第一个指针肯定已经在环内的某个节点上了，接下来这两个指针就在链表的环内旋转遍历，因为第一个指针比第二个指针每次都多走一步，所以它肯定会追上第二个指针。

      对于这里是不是一定能追上，我想应该有一个严格的证明，假设环上总共有n个节点，分别标号为0到n-1,如图3所示，并且第二个指针第一次到达环的入口节点时，第一个指针指向节点a, 则如果它们走了i 次后相遇，即i%n == (a + 2*i)*/n，则说明链表有环。

      因此，两个指针是不是一定能在环内相遇的问题就转化成了，证明存在一个正整数i,使i%n == (a + 2*i)*/n,其中（n>=2, a>=0并且a<n）的问题。由于我数论不好，对此问题一直没证明出来，所以在此请高手指教？

      用代码实现的方法，证实它确定可以判断出链表是否有环。

代码实现：

//判断单向链表是否有环
//输入参数：单链表的头指针
//输出参数：无
//返回值：有环返回true,无环返回false
bool IsLoop(SingleList *head)
{
	SingleList *firstPtr,*secondPtr;

	firstPtr = head;
	secondPtr = head;

	while(firstPtr&&firstPtr->next)
	{
		firstPtr = firstPtr->next->next;
		secondPtr = secondPtr->next;

		if(firstPtr == secondPtr)
		{
			return true;
		}
	}

	return false;
}

7  判断两个单向链表是否相交

思路：

图4  相交的单向链表

      考虑如果两个单向链表相交（如图4所示），那么两个链表中肯定有共同的节点。

      针对此问题， 最一般的思路就是判断一个链表的节点是否在另一个链表中存在。这种方法要双层循环实现，所以时间的复杂度为O（n²）。

      进一步研究相交链表的特性，发现如果相交，则两条链表的最后一个节点肯定相同。因此，只要判断两条链表的最后一个节点是不是相同就可以了。这种方法只需要遍历一遍每个链表找到它们的最终节点就可以了，所以算法的复杂度为O（n）。

代码实现：

//判断两条单向链表是否相交
//输入参数：两个单链表的头指针
//输出参数：无
//返回值：相交返回true,不相交返回false
bool IsIntersect(SingleList *head1,SingleList *head2)
{
	SingleList *firstPtr = head1,*secondPtr = head2;

	if((firstPtr == NULL) || (secondPtr == NULL))
	{
		return false;
	}
	//循环遍历第一个链表,找到最后一个元素
	while(firstPtr->next)
	{
		firstPtr = firstPtr->next;	
	}

	//循环遍历第二个链表，找到最后一个元素
	while(secondPtr->next)
	{
		secondPtr = secondPtr->next;	
	}

	if(firstPtr == secondPtr)
	{
		return true;
补充：综合编程 , 其他综合 ,