nbu 2429 Transfer stations

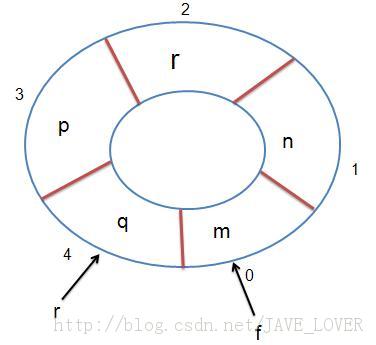
题目大意:
现在有一项工程,有n(n<=5000,编号1~n)个站点可以建立,建立i站点需要花费pi.
而假设a站点和b站点均建立了,那么可以获利C<a,b>,这样的关系有m个(m<=50000).
问建立那些站点可获得最大纯利润.
 
题目思路:
裸的最大权闭合图.
这种题型的建图有两种方法.
一:(建完后的图的原图完全不同)
(1)将所有边看成点(成为利润点),并各向构成这条边的两个点建立一条容量为正无穷大的边.
(3)用源点(建立一个超级源点)向所有利润点建立一条容量为其获利的边.
(2)将原来所有点(成为花费点),向汇点(建立一个超级汇点)建立一条容量为其花费的边.
这样之后就是要求出该图的最小割,而且最小割必然是割在和源点或者汇点相连的边上,因为其余的边容量均为无穷大.  www.zzzyk.com
通俗的说最小割的割集就是我们不需要的建立的站点的花费和无法获利的边.
这种方法的正确性,其实可以这样考虑,从源点到汇点必然是这样的路径: 源点--->利润边--->花费边--->汇点,
而最小割肯定是割在这三条边上容量最小的一条.
将问题转为最小割之后,由于最小割容量等于最大流,所以用所有利润边的获利和减去求得最大流即可.
 
二:(只需要在原图的基础上改进)
对于第一种我们可以分析,
点数=n+m+2,n最大是5000,m最大是50000,所以构造出来的图会有55002个点.
边数=n+m+m,大概11万条边.
显然这是一个 很庞大的图,效率并不好.
所以我们需要一个更好的建模方式.
(1)同样需要一个超级源点S,一个超级汇点T.
(2)源点连向所有点,容量为U (U为所有获利的和),称为零边.
(3)所有点连向汇点,容量为U+2*pi-di (di为所有所有和i相关联的边的权值和),称为差边.
ps:U的作用是为了使差边的容量非负.
这样我们可以看一下从源点到汇点的路径是什么样的.
假设原图中存在一条利润边a-->b
那么必然存在这样几条路径使得S和T连通.
S ---> a ---> T
S ---> b ---> T
S ---> a ---> b ---> T
S ---> b ---> a ---> T
为了使得S和T不连通,那么最小割可能为以下两种.
S ---> a 和 S ---> b ,即都割零边,割的容量为2U
a ---> T 和 b ---> T ,即都割差边,割的容量为2U+2*(pa+pb)-(va+vb)
S ---> a 和 b ---> a 和 b ---> T , 即割零边和差边,割的容量为2U+2*pb-vb+weight(a,b).
S ---> b 和 a ---> b 和 a ---> T , 即割零边和差边,割的容量为2U+2*pa-va+weight(a,b).
如果割零边,表示a站点和b站点都不建立,显然利润为0.
反之,a和b 都建立,利润应该是 weigt(a,b)-(pa+pb).
如果与a,与b关联的边均只有一条,即(a,b),那么va = vb = weigt(a,b).
那么割差边时,割的容量2U+2*(pa+pb)-(va+vb) =2U+2*(pa+pb)-2*weigt(a,b).
假设还有一割点c与a关联,且除a没有其他点和c关联.
1).假设c站点建立,那么多了一个割为c ---> T.
那么割的容量为 3U+2*(pa+pb+pc)-(va+vb+vc) = 3U+2*(pa+pb+pc)-2*(weigt(a,b)+weight(a,c)).
2).假设c站点不建立,那么多两个割为S ---> c 和 a ---> c
那么割的容量为 3U+2*(pa+pb) - (va+vb) + weight(a,c) 
  = 3U+2*(pa+pb)-2*weigt(a,b)-weight(a,c)+weight(a,c)
          = 3U+2*(pa+pb)-2*weigt(a,b)
同理可证当c或b还有其他关联边时也满足该式子.
又所以利润 = (nU-割[S,T])/2.
 
 
代码(一):
[cpp] 
#include <stdlib.h>  
#include <string.h>  
#include <stdio.h>  
#include <ctype.h>  
#include <math.h>  
#include <stack>  
#include <queue>  
#include <map>  
#include <set>  
#include <vector>  
#include <string>  
#include <iostream>  
#include <algorithm>  
using namespace std;  
  
#define ll long long  
#define ls rt<<1  
#define rs ls|1  
#define lson l,mid,ls  
#define rson mid+1,r,rs  
#define middle (l+r)>>1  
#define eps (1e-8)  
#define clr_all(x,c) memset(x,c,sizeof(x))  
#define clr(x,c,n) memset(x,c,sizeof(x[0])*(n+1))  
#define MOD 1000000009  
#define INF 0x3f3f3f3f  
#define PI acos(-1.0)  
#define _max(x,y) (((x)>(y))? (x):(y))  
#define _min(x,y) (((x)<(y))? (x):(y))  
#define _abs(x) ((x)<0? (-(x)):(x))  
#define getmin(x,y) (x= ((x)<0 || (y)<(x))? (y):(x))  
#define getmax(x,y) (x= ((y)>(x))? (y):(x))  
template <class T> void _swap(T &x,T &y){T t=x;x=y;y=t;}  
int TS,cas=1;  
const int M=60000+5;  
int n,m;  
  
struct sap{  
    typedef int type;  
    struct edge{  
        int to,next;  
        type flow;  
    }edg[999999];  
    int n,m;  
    int g[M],cur[M],pre[M];  
    int dis[M],gap[M];  
    int q[M],head,tail;  
    void init(int _n){n=_n,m=0,clr_all(g,-1);}  
    void insert(int u,int v,type f,type c=0){  
        edg[m].to=v,edg[m].flow=f,edg[m].next=g[u],g[u]=m++;  
        edg[m].to=u,edg[m].flow=0,edg[m].next=g[v],g[v]=m++;  
    }  
    bool bfs(int s,int t){  
        clr(gap,0,n),clr(dis,-1,n);  
        gap[dis[t]=0]++,dis[s]=-1;  
        for(q[head=tail=0]=t;head<=tail;){  
            int u=q[head++];  
            for(int i=g[u];i!=-1;i=edg[i].next){  
                edge& e=edg[i],ee=edg[i^1];  
                if(dis[e.to]==-1 && ee.flow>0){  
                    gap[dis[e.to]=dis[u]+1]++;  
                    q[++tail]=e.to;  
                }  
            }  
        }  
        return dis[s]!=-1;  
    }  
    type maxFlow(int s,int t){  
        if(!bfs(s,t)) return 0;  
        type res=0,a;  
        int i;  
        for(i=0;i<n;i++) cur[i]=g[i];  
        pre[s]=s,cur[s]=g[s],cur[t]=g[t];  
        for(int u=s;dis[s]<n;){  
            if(u==t){  
                for(a=-1;u!=s;u=pre[u])  
                    getmin(a,edg[cur[pre[u]]].flow);  
                for(u=t;u!=s;u=pre[u]){

补充：软件开发 , C++ ,