hdu4291之矩阵快速幂
A Short problem
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1110 Accepted Submission(s): 436
Problem Description
According to a research, VIM users tend to have shorter fingers, compared with Emacs users.
Hence they prefer problems short, too. Here is a short one:
Given n (1 <= n <= 1018), You should solve for
g(g(g(n))) mod 109 + 7
where
g(n) = 3g(n - 1) + g(n - 2)
g(1) = 1
g(0) = 0
Input
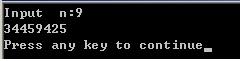
There are several test cases. For each test case there is an integer n in a single line.
Please process until EOF (End Of File).
Output
For each test case, please print a single line with a integer, the corresponding answer to this case.
Sample Input
0
1
2
Sample Output
0
1
42837
分析:假设g(g(g(n)))=g(x),x可能非常大,但是由于mod 10^9+7,所以可以求出x的循环节
求出x的循环节后,假设g(g(g(n)))=g(x)=g(g(y)),即x=g(y),y也可能非常大,但是由x的循环节可以求出y的循环节
所以最终结果只要进行矩阵快速幂即可求出
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;
const int mod1=1000000007;//求结果的循环节
const int mod2=222222224;//第1层的循环节,假设g(g(g(n)))=g(x),即mod2是x的循环节
const int mod3=183120;//第2层的循环节假设g(g(g(n)))=g(g(y)),即mod3是y的循化节
__int64 array[2][2],sum[2][2];
void MatrixMult(__int64 a[2][2],__int64 b[2][2],int mod){
__int64 c[2][2]={0};
for(int i=0;i<2;++i){
for(int j=0;j<2;++j){
for(int k=0;k<2;++k){
c[i][j]+=a[i][k]*b[k][j];
}
}
}
for(int i=0;i<2;++i){
for(int j=0;j<2;++j)a[i][j]=c[i][j]%mod;
}
}
__int64 Matrix(__int64 k,int mod){
array[0][0]=3,array[1][1]=0;
array[0][1]=array[1][0]=1;
sum[0][0]=sum[1][1]=1;
sum[0][1]=sum[1][0]=0;
while(k){
if(k&1)MatrixMult(sum,array,mod);
MatrixMult(array,array,mod);
k>>=1;
}
return sum[0][0];
}
int main(){
/*__int64 a=0,b=1;
for(int i=2;;++i){//求循环节
a=(b*3+a)%mod2;
a=a^b;
b=a^b;
a=a^b;
if(a == 0 && b == 1){cout<<i-1<<endl;break;}//i-1=222222224
}*/
__int64 n;
while(scanf("%I64d",&n)!=EOF){
if(n>=2)n=Matrix(n-1,mod3);
if(n>=2)n=Matrix(n-1,mod2);
if(n>=2)n=Matrix(n-1,mod1);
printf("%I64d\n",n);
}
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;
const int mod1=1000000007;//求结果的循环节
const int mod2=222222224;//第1层的循环节,假设g(g(g(n)))=g(x),即mod2是x的循环节
const int mod3=183120;//第2层的循环节假设g(g(g(n)))=g(g(y)),即mod3是y的循化节
__int64 array[2][2],sum[2][2];
void MatrixMult(__int64 a[2][2],__int64 b[2][2],int mod){
__int64 c[2][2]={0};
for(int i=0;i<2;++i){
for(int j=0;j<2;++j){
for(int k=0;k<2;++k){
c[i][j]+=a[i][k]*b[k][j];
}
}
}
for(int i=0;i<2;++i){
for(int j=0;j<2;++j)a[i][j]=c[i][j]%mod;
}
}
__int64 Matrix(__int64 k,int mod){
array[0][0]=3,array[1][1]=0;
array[0][1]=array[1][0]=1;
sum[0][0]=sum[1][1]=1;
sum[0][1]=sum[1][0]=0;
while(k){
if(k&1)MatrixMult(sum,array,mod);
MatrixMult(array,array,mod);
k>>=1;
}
return sum[0][0];
}
int main(){
/*__int64 a=0,b=1;
for(int i=2;;++i){//求循环节
a=(b*3+a)%mod2;
a=a^b;
b=a^b;
a=a^b;
if(a == 0 && b == 1){cout<<i-1<<endl;break;}//i-1=222222224
}*/
__int64 n;
while(scanf("%I64d",&n)!=EOF){
if(n>=2)n=Matrix(n-1,mod3);
if(n>=2)n=Matrix(n-1,mod2);
if(n>=2)n=Matrix(n-1,mod1);
printf("%I64d\n",n);
}
return 0;
}
补充:软件开发 , C++ ,