微软等数据结构与算法面试100题第十一题

第十一题
题目：
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图，父子节点之间的连线看成是双向的，
我们姑且定义"距离"为两节点之间边的个数。
写一个程序，
求一棵二叉树中相距最远的两个节点之间的距离。

分析：
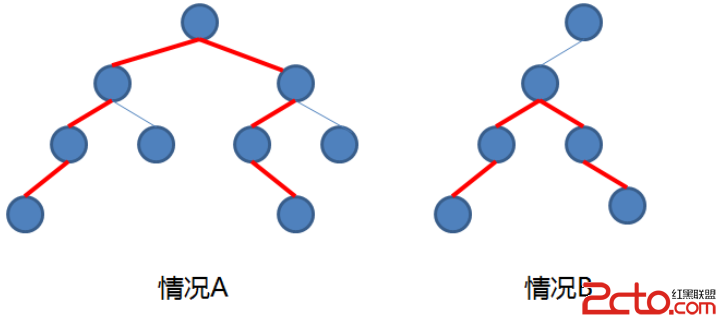
对本题而言，有上面两种情况，一个是最大长度的节点里面没有根节点，一个是有根节点。
如何求解树中节点的最大距离？-->转换成求解每个节点的左子树的深度和右子树的深度问题，可以通过求解每个节点的左右子树的深度，然后将左右深度之和作为最大长度，
然后更新最大长度。
对于图A，根节点的左子树的深度为3，右子树的深度为3，因此最大长度为6，
对于图B，不妨设根节点的左儿子节点为T，T的左子树的深度为2，右子树的深度为2，因此最大长度为4。
所以，我们只需要求解每个节点的左子树深度和右子树深度，然后不断更新最大长度即可。

代码：构建的二叉树为图A
[cpp]
#include<iostream>
using namespace std;

struct nodeBTree
{
    nodeBTree * nodeBTreeLeft;
    nodeBTree * nodeBTreeRight;
    int maxDepthLeft;
    int maxDepthRight;
    int index;
};

int maxNum(int comp_a, int comp_b)
{
    if(comp_a>comp_b)
        return comp_a;
    else
        return comp_b;
}
void updateMaxDepthLR(nodeBTree * BTreeHead, int &MaxLength)
{
    int maxDepthLC = 0;
    int maxDepthRC = 0;
    if(NULL==BTreeHead){return;}
    if(NULL!=BTreeHead->nodeBTreeLeft)
    {
        updateMaxDepthLR(BTreeHead->nodeBTreeLeft,MaxLength);
        maxDepthLC = max(BTreeHead->nodeBTreeLeft->maxDepthLeft,BTreeHead->nodeBTreeLeft->maxDepthRight);
        BTreeHead->maxDepthLeft = maxDepthLC + 1;
    }
    else
    {
        BTreeHead->maxDepthLeft = 0;
    }
    if(NULL!=BTreeHead->nodeBTreeRight)
    {
        updateMaxDepthLR(BTreeHead->nodeBTreeRight,MaxLength);
        maxDepthRC = max(BTreeHead->nodeBTreeRight->maxDepthLeft,BTreeHead->nodeBTreeRight->maxDepthRight);
        BTreeHead->maxDepthRight = maxDepthRC + 1;
    }
    else
    {
        BTreeHead->maxDepthRight = 0;
    }
    if(BTreeHead->maxDepthRight + BTreeHead->maxDepthLeft >MaxLength)
        MaxLength = BTreeHead->maxDepthRight + BTreeHead->maxDepthLeft;
}
int main()
{
    #pragma region construct the binary tree //图A
    nodeBTree* a = new struct nodeBTree();
    a->index = 0;
    nodeBTree* b = new struct nodeBTree();
    b->index = 1;
    nodeBTree* c = new struct nodeBTree();
    c->index = 2;
    nodeBTree* d = new struct nodeBTree();
    d->index = 3;
    nodeBTree* e = new struct nodeBTree();
    e->index = 4;
    nodeBTree* f = new struct nodeBTree();
    f->index = 5;
    nodeBTree* g = new struct nodeBTree();
    g->index = 6;
    nodeBTree* h = new struct nodeBTree();
    h->index = 7;
    nodeBTree* i = new struct nodeBTree();
    i->index = 8;

    a->nodeBTreeLeft = b;
    a->nodeBTreeRight = c;
    b->nodeBTreeLeft = d;
    b->nodeBTreeRight = e;
    c->nodeBTreeLeft = f;
    c->nodeBTreeRight = g;
    d->nodeBTreeLeft = h;
    d->nodeBTreeRight =NULL;
    e->nodeBTreeLeft = NULL;
    e->nodeBTreeRight = NULL;
    f->nodeBTreeLeft = NULL;
    f->nodeBTreeRight = i;
    g->nodeBTreeLeft = NULL;
    g->nodeBTreeRight = NULL;
    h->nodeBTreeLeft = NULL;
    h->nodeBTreeRight = NULL;
    i->nodeBTreeLeft = NULL;
    i->nodeBTreeRight = NULL;
    #pragma endregion

    int MaxLength = 0;
    updateMaxDepthLR(a,MaxLength);

    //输出update的结果
    cout<<"a->maxDepthLeft: "<<a->maxDepthLeft<<endl;
    cout<<"b->maxDepthLeft: "<<b->maxDepthLeft<<endl;
    cout<<"c->maxDepthLeft: "<<c->maxDepthLeft<<endl;
    cout<<"d->maxDepthLeft: "<<d->maxDepthLeft<<endl;
    cout<<"e->maxDepthLeft: "<<e->maxDepthLeft<<endl;
    cout<<"f->maxDepthLeft: "<<f->maxDepthLeft<<endl;
    cout<<"g->maxDepthLeft: "<<g->maxDepthLeft<<endl;
    cout<<"h->maxDepthLeft: "<<h->maxDepthLeft<<endl;
    cout<<"i->maxDepthLeft: "<<i->maxDepthLeft<<endl;

    cout<<"a->maxDepthRight: "<<a->maxDepthRight<<endl;
    cout<<"b->maxDepthRight: "<<b->maxDepthRight<<endl;
    cout<<"c->maxDepthRight: "<<c->maxDepthRight<<endl;
    cout<<"d->maxDepthRight: "<<d->maxDepthRight<<endl;
    cout<<"e->maxDepthRight: "<<e->maxDepthRight<<endl;
    cout<<"f->maxDepthRight: "<<f->maxDepthRight<<endl;
    cout<<"g->maxDepthRight: "<<g->maxDepthRight<<endl;
    cout<<"h->maxDepthRight: "<<h->maxDepthRight&l

补充：软件开发 , C++ ,

微软等数据结构与算法面试100题 第十一题

微软等数据结构与算法面试100题第十一题