三种线性时间排序算法 - C++实现

引言

注：由于没有启用任何公式编辑器，为表示方便：以下涉及时间复杂度表示时，其渐近符号用以下符号代替：

先来看一个定理：任意一个比较排序算法在最坏情况下，都需要做 $(nlgn)次的比较。其可用决策树模型加以证明，详见：《算法导论》第8章8.1节。

该定理指出了比较排序的时间复杂度下界，即没有比较更少的了。

故以下介绍的三种算法均不是基于比较的排序算法，其均对输入数据作了某种假设，即利用了具体数据的特点。

一、计数排序

1、问题描述：假设数组中的n个元素中的每一个都是介于0到k之间的整数，对其进行排序。此处k为某个正整数。

2、基本思想：对每一个输入元素x，利用它的所属范围大小为[0, k] ,确定出数组中小于x 的元素个数。由于x为正整数，则可以直接把x直接放到它在最终输出数组中的位置上。

3、算法描述：

输入：A[1...n], 输入数组；C[0...k]，提供临时存储区，初值：0 ---O(k)

输出：B[1...n]，存放排序结果

（1）求出输入数组A[]1...n]中，其值等于A[j]的元素个数，存放于对应的C[1...k]中：C[A[i]] = C[A[i]] + 1 ---O(n)

（2）求出输入数组A[]1...n]中，其值小于或等于A[j]的元素个数，迭代地存放于对应的C[1...k]中：C[j] = C[j-1] + C[j] ---O(K)

（3）经过前两步之后，C[i]中的值表示为：小于等于 i 的元素个数，即为 i 在A[1...n]中的最终位置，将其存放于B[1...n]中：B[C[A[j]]] = A[j], C[A[j]] = C[A[j]] - 1 （有可能存在想相等的元素） --- O(n)

4、时间复杂度：O(k) + O(n) + O(k) + O(n)，则总的运行时间为：@(k+n)，在实践中，当 k=O(n)时，其运行时间即为：@(n).

5、算法实现：

[cpp]
#include <stdio.h>
const int K = 5;
const int N = 6;
int input[N+1] = {-1, 2, 3, 4, 2 ,1, 5};
int output[N+1];
int count[K]={0};

void print(int array[], int n)
{
    for(int i = 1; i <=n; i++)
    {
        printf("%d ", array[i]);
    }
    printf("\n");
}
void countSort(int input[], int output[], int n)
{
    int i;
    for(i = 1; i <= n; i++)
    {//equal to input[i]
        count[input[i]] = count[input[i]] +1;
    }
    for(i = 1; i <= K; i++)
    {//less ro equal to i
        count[i] = count[i-1] + count[i];
    }
    for(i = n; i >= 1; i--) //form large to small to make sorting stable
    {
        output[count[input[i]]] = input[i];
        count[input[i]]--;
    }
}

int main()
{
    countSort(input, output, N);
    print(output, N);
    return 0;
}

#include <stdio.h>
const int K = 5;
const int N = 6;
int input[N+1] = {-1, 2, 3, 4, 2 ,1, 5};
int output[N+1];
int count[K]={0};

void print(int array[], int n)
{
for(int i = 1; i <=n; i++)
{
  printf("%d ", array[i]);
}
printf("\n");
}
void countSort(int input[], int output[], int n)
{
int i;
for(i = 1; i <= n; i++)
{//equal to input[i]
  count[input[i]] = count[input[i]] +1;
}
for(i = 1; i <= K; i++)
{//less ro equal to i
  count[i] = count[i-1] + count[i];
}
for(i = n; i >= 1; i--) //form large to small to make sorting stable
{
  output[count[input[i]]] = input[i];
  count[input[i]]--;
}
}

int main()
{
countSort(input, output, N);
print(output, N);
return 0;
}

二、基数排序

1、问题描述：给定n个d位数，每一位可能的取值有k中，对其进行排序。如，4个三位数：123，367,124,756，此时n=4, d=3，k值为10.

2、基本思想：首先按最低有效位数字进行排序，收集结果；然后按次低位有效位数字排序，收集其结果，依次类推，重复这个过程，直到对所有的d位数字都进行了排序。

看个例子（来自算法导论8.3的示例,P100）：

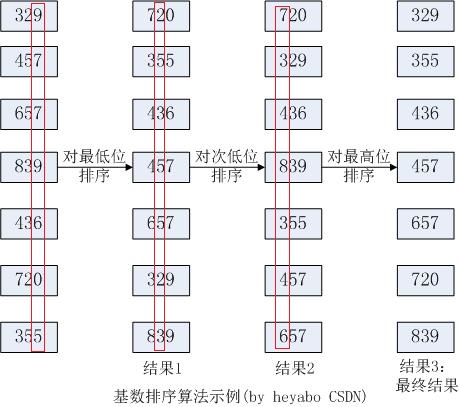
注意：对每一位的排序必须是一个稳定的排序，否则排序可能不正确。如上图在对最高位排序时，起初436在457的前面，由于最高位都是4，故此次排序两个数的最高位相等，如果不是稳定的排序，结果457可能会排到436的前面，这样结果就不对了。而稳定的排序则可以保证排完后，436仍然在457的前面。

3、算法描述：

输入数组：A[1...n]

RADIX-SORT(A, d)

for i <- 1 to d

do use a stable sort to sort array A on digit i //可以选择计数排序

4、时间复杂度：由一中的计数排序可知，对每一位的排序时间为：@(k+n)，此处共执行d遍，故时间复杂度：@(d*(k+n))，当d为常数、k=O(n)时，基数排序有线性运行时间：@(n)。更一般且更具体的分析可以参加《算法导论》的引理8.3和8.4，P101，其详细分析了：如何将每个关键字分解成若干位以及那些情况下时间复杂度最佳。此处只介绍一些结论与如何实现之。

5、算法实现：

[cpp]
#include <stdio.h>
#include <math.h>
const int N = 7;
const int D = 3;
const int K = 10;
int count[K] = {0};
//int input[N+1] = {-1, 329, 457, 657, 839, 436, 720, 355};
int output[D+1][N+1]={{-1, 329, 457, 657, 839, 436, 720, 355}};

void print(int array[], int n)
{
    for(int i = 1; i <=n; i++)
    {
        printf("%d ", array[i]);
    }
    printf("\n");
}
int getDigit(int number, int d)
{
    if(d > D)return -1;
    return number%(int)pow(10,d) / (int)pow(10,d-1);
}
void countSort(int input[], int output[], int n, int d)
{
    int i;
    int digit;
    for(i = 1; i <= n; i++)
    {
        digit = getDigit(input[i],d);
        count[digit] = count[digit] +1;
    }
    for(i = 1; i <= K; i++)
    {
        count[i] = count[i-1] + count[i];
    }
    for(i = n; i >= 1; i--) //form large to small to make sorting stable
    {
        digit = getDigit(input[i],d);
        output[count[digit]] = input[i];
        count[digit]--;
    }
}
void initDataStruct(int count[])
{

补充：软件开发 , C++ ,