动态规划-装配线调度

问题描述：

一个找出通过工厂装配线的最快方式的制造问题。共有两条装配线，每一条装配线上有n个装配站，编号为j = 0, 1, … , n – 1。装配线i(i = 0或1)，在装配站S[i][j]上所需的装配时间记为a[i][j]。一个汽车底盘进入工厂，然后进入装配线i的进入时间为e[i]，在通过一条线的第j个装配站后，这个底盘来到任一条线的第(j + 1)个装配站。如果留在相同的装配线上，则没有移动的开销；如果在装配站S[i][j]后，它移动到了另一条线上，则花费时间t[i][j]。在离开一条线的第n个装配站后，完成的汽车离开装配线i的离开时间为x[i] 。

状态转移方程：

代码实现：

[cpp]
//动态规划，工厂装配线
#include<iostream>
using namespace std;
//e1,e2是两条装配生产线的输入耗费x1，x2是输出耗费，a1[i]是第一条生产线的第i个站耗时，t1，t2记录了两条生产线转换时耗时
//f1[i]为记录第一条生产线上第i个站生产耗时最少时间，L1[i]记录了第一条生产线上第i个站生产耗时最少时，前一站是那条生产线上的
//length为每条生产线上的站数
void FastWay(int e1,int e2,int *a1,int *a2,int x1,int x2,int *f1,int *f2,int *L1,int *L2,int &L,int *t1,int *t2,int length)
{
    f1[1]=e1+a1[1];
    f2[1]=e2+a2[1];
    int i;
    for(i=2;i<length;i++)
    {
        if(f1[i-1]+a1[i]<f2[i-1]+a1[i]+t2[i-1])
        {
            f1[i]=f1[i-1]+a1[i];
            L1[i]=1;
        }
        else
        {
            f1[i]=f2[i-1]+a1[i]+t2[i-1];
            L1[i]=2;
        }
        if(f2[i-1]+a2[i]<f1[i-1]+a2[i]+t1[i-1])
        {
            f2[i]=f2[i-1]+a2[i];
            L2[i]=2;
        }
        else
        {
            f2[i]=f1[i-1]+a2[i]+t1[i-1];
            L2[i]=1;
        }
    }
    //利用f1[length]来存储所用最短时间
    if(f1[length-1]+x1<f2[length-1]+x2)
    {
        f1[length]=f1[length-1]+x1;
        L=1;
    }
    else
    {
        f1[length]=f2[length-1]+x2;
        L=2;
    }

}
//输出最短时间以及所需要的路线
void Printanswser(int *L1,int *L2,int L,int length,int *f1)
{
    int i=L;
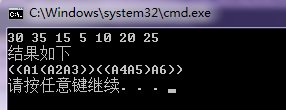
    cout<<"the fast time is : "<<f1[length+1]<<endl;
    cout<<"the station : "<<length<<" is on line: "<<i<<endl;
    int j;
    for(j=length;j>=2;j--)
    {
        if(i==1)
        {
            i=L1[j];
        }
        else
        {
            i=L2[j];
        }
        cout<<"the station : "<<j-1<<" is on line: "<<i<<endl;
    }
}
int main()
{
    int e1=2,e2=4,x1=3,x2=2;
    int a1[8]={0,7,9,3,4,8,4};
    int a2[8]={0,8,5,6,4,5,7};
    int t1[6]={0,2,3,1,3,4};
    int t2[6]={0,2,1,2,2,1};
    int f1[8],f2[7],L1[7],L2[7],L;
    FastWay(e1,e2,a1,a2,x1,x2,f1,f2,L1,L2,L,t1,t2,7);
    Printanswser(L1,L2,L,6,f1);
    return 0;
}

//动态规划，工厂装配线
#include<iostream>
using namespace std;
//e1,e2是两条装配生产线的输入耗费x1，x2是输出耗费，a1[i]是第一条生产线的第i个站耗时，t1，t2记录了两条生产线转换时耗时
//f1[i]为记录第一条生产线上第i个站生产耗时最少时间，L1[i]记录了第一条生产线上第i个站生产耗时最少时，前一站是那条生产线上的
//length为每条生产线上的站数
void FastWay(int e1,int e2,int *a1,int *a2,int x1,int x2,int *f1,int *f2,int *L1,int *L2,int &L,int *t1,int *t2,int length)
{
f1[1]=e1+a1[1];
f2[1]=e2+a2[1];
int i;
for(i=2;i<length;i++)
{
  if(f1[i-1]+a1[i]<f2[i-1]+a1[i]+t2[i-1])
  {
   f1[i]=f1[i-1]+a1[i];
   L1[i]=1;
  }
  else
  {
   f1[i]=f2[i-1]+a1[i]+t2[i-1];
   L1[i]=2;
  }
  if(f2[i-1]+a2[i]<f1[i-1]+a2[i]+t1[i-1])
  {
   f2[i]=f2[i-1]+a2[i];
   L2[i]=2;
  }
  else
  {
   f2[i]=f1[i-1]+a2[i]+t1[i-1];
   L2[i]=1;
  }
}
//利用f1[length]来存储所用最短时间
if(f1[length-1]+x1<f2[length-1]+x2)
{
  f1[length]=f1[length-1]+x1;
  L=1;
}
else
{
  f1[length]=f2[length-1]+x2;
  L=2;
}

}
//输出最短时间以及所需要的路线
void Printanswser(int *L1,int *L2,int L,int length,int *f1)
{
int i=L;
cout<<"the fast time is : "<<f1[length+1]<<endl;
cout<<"the station : "<<length<<" is on line: "<<i<<endl;
int j;
for(j=length;j>=2;j--)
{
  if(i==1)
  {
   i=L1[j];
  }
  else
  {
   i=L2[j];
  }
  cout<<"the station : "<<j-1<<"

补充：软件开发 , C++ ,