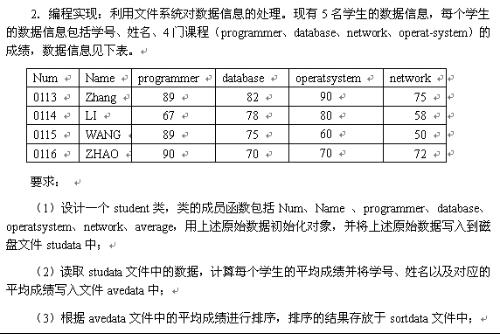
spoj 1811 Longest Common Substring (后缀自动机)

 

题意：lcs。。求两个字符串的最长公共连续子串

 

解题思路：后缀自动机解法。对第一个字符串构造sam，将第二个字符串的字符依次加入sam去匹配。假如我们匹配s2[i]时，匹配到的最大值为temp，在sam上匹配到的位置为p，那当加入s2[i+1]时应该如何更新呢？显然，如果p有指向s2[i]的儿子，temp[i+1] = temp[i] +１，p更新为p->son[k]。如果没有，那么p就沿着fa走，直到p有指向s2[i+1]的儿子，或者p走到NULL。假如p走到了NULL，那么在s2[i+1]这个位置，我们没有匹配到任何字符，故temp[i+1] = 0 , p 走到root。否则，temp[i+1] = val[p] + 1,p更新为p->son[k]。这里temp[i+1]是不能更新为val[q]的（设q=p->son[k]），因为val[q] 并不一定等于val[p] +１，而s2[i]我们只能匹配到p（p沿着fa走，那么很显然，这一路过来的p都能与s2[i]匹配）。

 

#include<stdio.h>  
#include<string.h>  
#include<algorithm>  
using namespace std ;  
  
const int maxn = 250010 ;  
  
struct sam {  
    int fa[maxn<<1] , c[26][maxn<<1] , val[maxn<<1] ;  
    int dp[maxn<<1] , tot , last ;  
  
    inline int new_node ( int step ) {  
        int i ;  
        val[++tot] = step ;  
        fa[tot] = 0 ;  
        for ( i = 0 ; i < 26 ; i ++ ) c[i][tot] = 0 ;  
        return tot ;  
    }  
  
    void add ( int k ) {  
        int i , p = last ;  
        int np = new_node ( val[p] + 1 ) ;  
        while ( p && !c[k][p] ) c[k][p] = np , p = fa[p] ;  
        if ( !p ) fa[np] = 1 ;  
        else {  
            int q = c[k][p] ;  
            if ( val[p] + 1 == val[q] ) fa[np] = q ;  
            else {  
                int nq = new_node ( val[p] + 1 ) ;  
                for ( i = 0 ; i < 26 ; i ++ )  
                    c[i][nq] = c[i][q] ;  
                fa[nq] = fa[q] ;  
                fa[q] = fa[np] = nq ;  
                while ( p && c[k][p] == q ) c[k][p] = nq , p = fa[p] ;  
            }  
        }  
        last = np ;  
    }  
  
    void build ( char *s , int len ) {  
        tot = 0 ;  
        last = new_node ( 0 ) ;  
        int i ;  
        for ( i = 0 ; i < len ; i ++ )  
            add ( s[i] - 'a' ) ;  
    }  
  
    int solve ( char *s ) {  
        int len = strlen ( s ) , i ;  
        int ret = 0 , pre = 0 ;  
        int p = 1 ;  
        memset ( dp , 0 , sizeof ( dp ) ) ;  
        for ( i = 0 ; i < len ; i ++ ) {  
            int k = s[i] - 'a' ;  
            if ( c[k][p] ) pre ++ , p = c[k][p] ;  
            else {  
                while ( !c[k][p] && p ) p = fa[p] ;  
                if ( p ) pre = val[p] + 1 , p = c[k][p] ;  
                else p = 1 , pre = 0 ;  
            }  
            ret = max ( ret , pre ) ;  
        }  
        return ret ;  
    }  
} suf ;  
  
char s[maxn] ;  
  
int main () {  
    while ( scanf ( "%s" , s ) != EOF ) {  
        suf.build ( s , strlen ( s ) ) ;  
        scanf ( "%s" , s ) ;  
        printf ( "%d\n" , suf.solve ( s ) ) ;  
    }  
    return 0 ;  
}  

 

补充：软件开发 , C++ ,