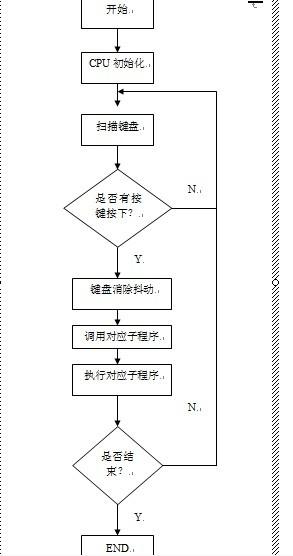
HDU 3644 A Chocolate Manufacturer's Problem(模拟退火)

题目：一个任意多边形，判断是否能放入一个半径为r的圆
一开始以为是半平面交，果断看大家的提交时间和代码长度就不像是，不过还是提交了一发，果断WA.
后来被昀昀科普了，凹多边形是不可以这么求的。凹多边形可能没有核，向内推近r后求核，显然是不对的。
点不是很多，那就只有模拟退火了，貌似不是只有。。。
要写这题，首先还得写个判断点是否在多边形内，因为以前写得太矬，打算重新写一个，然后就折腾了一晚上，各种错误，老是用直线去代替线段。有了这个判断，便可以开始模拟退火
模拟退火关键问题在于火候怎么把握，一开始尝试选取n个点，步长每次减小1/10，精度控制在1e-3,竟然TLE，看了网上的代码，也是这么多。然后开始各种尝试，果断减小选取的点数。各种WA,TLE无语。。。
有位好心的ACMER，给了一组数据
4
0 0
0 2
2 2
2 0
1
一般如果在判断的时候要求精度太高的话，这组数据过不了，果断不原本1e-8的精度改成1e-3，一通乱改之后，可以说是勉强通过了这组数据。
大清早的起来又是刷屏，各种尝试火候，最终还是刷进了200ms
最多选 20个点，每个点走5步，步长为原来的0.55，之前的TLE主要原因就是那组数据出不来，而且会WA。
[cpp]
#include<iostream>
#include<fstream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<string>
#include<vector>
#include<ctime>
#include<sstream>
#include<cassert>
#define LL long long
#define eps 1e-7
#define zero(a) fabs(a)<eps
#define inf 1<<30
#define N 20
#define pi acos(-1.0)
using namespace std;
struct Point{
    double x,y;
    double val;
}p[100],tp[100],pre,cur;
struct Segment{
    Point a,b;
};
int n;
inline double xmul(Point p0,Point p1,Point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
inline double dist(Point p1,Point p2){
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
//求点到线段距离
inline double Dist_Point_Seg(Point p,Point a,Point b){
    Point t=p;
    t.x+=a.y-b.y;t.y+=b.x-a.x;
    if(xmul(a,t,p)*xmul(b,t,p)>eps)
        return dist(p,a)+eps<dist(p,b)?dist(p,a):dist(p,b);
    else
        return fabs(xmul(p,a,b))/dist(a,b);
}
inline bool online(Point p1,Point p2,Point p){
    if(zero(xmul(p1,p2,p))&&((p.x-p1.x)*(p.x-p2.x)<eps&&(p.y-p1.y)*(p.y-p2.y)<eps))
        return true;
    return false;
}
inline bool across(Segment s1,Segment s2){
    if(xmul(s1.a,s1.b,s2.a)*xmul(s1.a,s1.b,s2.b)<eps)
        if(xmul(s2.a,s2.b,s1.a)*xmul(s2.a,s2.b,s1.b)<eps)
            return true;
    return false;
}
inline bool Parallel(Segment s1,Segment s2){
    return zero((s1.a.x-s1.b.x)*(s2.a.y-s2.b.y)-(s2.a.x-s2.b.x)*(s1.a.y-s1.b.y));
}
//判断点是否在多边形内
inline bool In_Polygon(Point cen){
    int cnt=0;
    Segment s,e;
    s.a=cen;s.b.y=cen.y;s.b.x=20000.0;
    for(int i=0;i<n;i++){
        e.a=p[i];e.b=p[i+1];
        if(online(p[i],p[i+1],cen)) return false;
        if(zero(p[i].y-p[i+1].y)) continue;
        if(online(s.a,s.b,p[i])){
            if(p[i].y>p[i+1].y) cnt++;
        }
        else if(online(s.a,s.b,p[i+1])){
            if(p[i+1].y>p[i].y) cnt++;
        }
        else if(across(s,e))
            cnt++;
    }
    return cnt&1;
}
inline void Get_Min_Dist(Point &cur){
    double ret=inf;
    for(int i=0;i<n;i++)
       ret=min(ret,Dist_Point_Seg(cur,p[i],p[i+1]));
    cur.val=ret;
}
int main(){
    double r,best[105];
    srand(time(NULL));
    while(scanf("%d",&n)!=EOF&&n){
        double maxx=0,maxy=0,minx=inf,miny=inf;
        for(int i=0;i<n;i++){
            scanf("%lf%lf",&p[i].x,&p[i].y);
            maxx = maxx>p[i].x?maxx:p[i].x;
            maxy = maxy>p[i].y?maxy:p[i].y;
            minx = minx<p[i].x?minx:p[i].x;
            miny = miny<p[i].y?miny:p[i].y;
        }
        p[n]=p[0];
        scanf("%lf",&r);
        int m=min(n,N);
        for(int i=0;i<m;i++){
            tp[i].x=(p[i].x+p[i+1].x)/2;
            tp[i].y=(p[i].y+p[i+1].y)/2;
            tp[i].val=0;
        }
        double step=sqrt((maxx-minx)*(maxx-minx)+(maxy-miny)*(maxy-miny))/2;
        bool flag=false;
        while(step>1e-3&&!flag){
            for(int i=0;i<m&&!flag;i++){
                for(int j=0;j<5&&!flag;j++){
                    double angle=rand();
              &n

补充：软件开发 , C++ ,