经典回溯问题-----旅行员售货问题

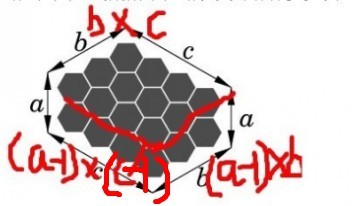
问题：某售货员要到若干城市去推销商品，已知各城市之间的路程（旅费），他要选定一条从驻地出发，经过每个城市一遍，最后回到驻地的路线，使总的路程（总旅费）最小。

以上图为例：售货员要从1开始经过2，3，4又返回1。

给我的感觉就是一个排列问题。在进行计算排列的同时要判断是否该排列有必要进行下去，因为可能在中途就可以判断这样肯定得不到我们想要的结果，此时采用回溯。

代码实现：

<span style="font-size:18px">/* 
*   售货员问题----回溯处理 
*   日期: 2013-11-07  
*/  
#include<iostream>  
using namespace std;  
  
#define MAX  1024  
  
int N=4;//可以自己输入，这里我就指定了，并且在init()中设定了所有点的Cost[][];  
int Cost[MAX][MAX];//记录任意两点的运费或代价  
int bestCost=MAX;//记录目前最少运费或代价  
int currentCost;//当前运费或代价  
int current[MAX];//当前路径  
int best[MAX];//记录最佳路径  
  
void swap(int& a,int& b)  
{  
    int temp=a;  
    a=b;  
    b=temp;  
}  
  
void backtrack(int t)//其实就是一个排列问题。。。  
{  
    int j;  
    if(t==N)//到了最后一层。。  
    {  
        if(Cost[current[t-1]][current[t]]+Cost[current[t]][1]+currentCost<bestCost)  
        {  
            bestCost=Cost[current[t-1]][current[t]]+Cost[current[t]][1]+currentCost;  
            for(j=1;j<=N;j++)  
            {  
                best[j]=current[j];  
            }  
        }  
    }  
      
    for(j=t;j<=N;j++)//排列。。。  
    {  
        swap(current[t],current[j]);  
        if(Cost[current[t-1]][current[t]]+currentCost<bestCost)//其实currentCost就是包括了1-->(t-1)的代价或运费  
        {  
            currentCost+=Cost[current[t-1]][current[t]];  
            backtrack(t+1);//递归回溯  
            currentCost-=Cost[current[t-1]][current[t]];  
        }  
        swap(current[t],current[j]);  
    }  
}  
  
void init()  
{  
     Cost[1][1]=0;  
     Cost[1][2]=30;  
     Cost[1][3]=6;  
     Cost[1][4]=4;  
  
     Cost[2][1]=30;  
     Cost[2][2]=0;  
     Cost[2][3]=5;  
     Cost[2][4]=10;  
  
     Cost[3][1]=6;  
     Cost[3][2]=5;  
     Cost[3][3]=0;  
     Cost[3][4]=20;  
  
     Cost[4][1]=4;  
     Cost[4][2]=10;  
     Cost[4][3]=20;  
     Cost[4][4]=0;  
}  
void main()  
{  
     init();  
  
     int i;  
     for(i=1;i<=N;i++)  
     {  
         current[i]=i;  
     }  
  
     backtrack(2);//树的第一层已经找到了，所以从第二层开始  
  
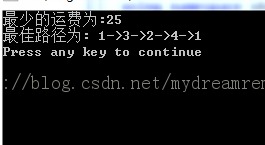
     cout<<"最少的运费为:"<<bestCost<<endl;  
     cout<<"最佳路径为: ";  
     for(i=1;i<=N;i++)  
     {  
         cout<<best[i]<<"->";  
     }  
     cout<<best[1]<<endl;  
}</span>

补充：软件开发 , C++ ,