Codeforces Round #133 (Div. 2)

感谢Dshawn的指导~~~~~~~
A. Tiling with Hexagons
给出a,b,c，根据图中的形状判断有多少块。

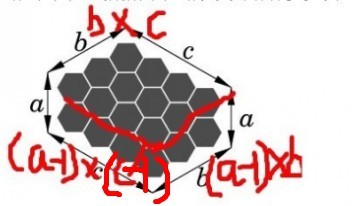
分为三个部分，总和就是b*c+(a-1)*(b+c-1)
也可以是不断向内一层层的分解。
最外层为2*(b+c+a)-6。
而里面一层为a-1,b-1,c-1,但是注意如果出现边为1的话，就不能这么统计了
不过边为1刚好就是一个矩形
[cpp]
while(a>1&&b>1&&c>1){
ans+=2*(a+b+c)-6;
a--;b--;c-;;
}
ans+=a*b*c;

B. Forming Teams
有N个人，组成两队比赛，每一队中不能有敌对状态。
由于每个人最多有两个敌对的，所以要么是单链，要么是简单的环，要么就是孤立状态。
孤立状态肯定不用考虑，随便往哪队放都可以
对于单链也不需要考虑，因为总是可以完整的分为两队
对于环先考虑偶数环，两两交错，也是可以分为两队
但是奇数环就不可以了，总有一个人首尾相接，不能去任何一队
所以结果就是如果有奇数环，总数减1，最后还需要判断奇偶性

C. Hiring Staff
开始是固定的，K为几，那么就得有K个人从第一天开始，然后前n天都不用考虑，不过得有一个人去交接钥匙，贪心处理，总是尽可能靠后，那就是第n天，从第n+1天只有一个人上班，如果k>1的话，就需要安排k--1个人从n+1天开始，如果k为1，那么就是从2*n-1去交接钥匙。总之每一个人都尽可能靠后，贪心模拟一下，直到第n+m+1天第一批人回来上班。
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
using namespace std;
int n,m,k;
vector<int>v;
int main(){
    while(scanf("%d%d%d",&n,&m,&k)!=EOF){
        v.clear();
        for(int i=0;i<k;i++)
            v.push_back(1);
        v.push_back(n);
        for(int i=1;i<k;i++)
            v.push_back(n+1);
        int l=2*n;
        if(k==1)
            l--;
        while(l<n+m+1){
            v.push_back(l);
            if(l+1==n+m+1) break;
            for(int i=1;i<k;i++)
                v.push_back(l+1);
            l+=n;
            if(k==1) l--;
        }
        printf("%d\n%d",v.size(),v[0]);
        for(int i=1;i<v.size();i++)
            printf(" %d",v[i]);
        puts("");
    }
    return 0;
}

D. Spider's Web
直接对于每一个区域，每一个小扇形进行枚举，二分找到对于两边的数目，比较
感觉这样不是很慢吗，哎。。。。。n*k，1000*100000*log(100000
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
#define pb(a) push_back(a)
#define ub(v,a) upper_bound(v.begin(),v.end(),a)
using namespace std;

int main(){vector <int> v[1001];
    int n,k,r;
    while(scanf("%d",&n)!=EOF){
        for(int i=1;i<=n;i++){
            v[i].clear();
            scanf("%d",&k);
            while(k--){
                scanf("%d",&r);
                v[i].pb(r);
            }
            sort(v[i].begin(),v[i].end());
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            int pre=i-1; pre=pre==0?n:pre;
            int next=i+1; next=next==n+1?1:next;
            for(int j=1;j<v[i].size();j++){
                int x=ub(v[pre],v[i][j])-ub(v[pre],v[i][j-1]);
                int y=ub(v[next],v[i][j])-ub(v[next],v[i][j-1]);
                if(x!=y) ans++;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

E. Martian Luck
有个重要的结论：在k进制下个位数字之和相当于那个数字转化成十进制以后mod(k-1)，0的话就是k-1
那么就能直接处理了，取前i项和的模数。用map记录，然后遍历一遍，就可以了。
不过由于k-1,0都最终记为0，所以这里要处理一下，如果b既不是0，也不是k-1的话，那就无所谓了。
我们通过原数据，找一下所有0的数目，因为这个比较方便，
那么如果b就是0，那么就是我们最后统计的数目
如果b为k-1那么我们要把原来统计的去掉b为0的情况。
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
#define pb(a) push_back(a)
#define ub(v,a) upper_bound(v.begin(),v.end(),a)
using namespace std;
int sum[100005],a[1

补充：软件开发 , C++ ,