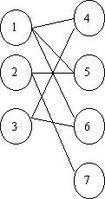
最长公共子序列问题
最长公共子序列问题很早就在很多论坛上见过,前几天看到一个人发了一篇帖子,心血来潮就去看算法导论上的动态规划部分,关于这个问题不再细述,直接贴C++实现的具体代码了。
[cpp]
//做大公共子序列问题
#pragma once
#include <string>
using std::string;
#define OVER 1 //书中使用箭头符号表示的,这里用宏代替
#define LEFT 2
#define LEFTOVER 3
class LCS
{
private:
string sX; //用于存储子序列
string sY;
int **c; //这两个二维指针是为了维护一个动态的表格,后面会根据这个表的来递归生成最长公共子序列
int **b;
int m; //分别表示两个字符串的长度,为了和书上伪代码一致就没有改动
int n;
public:
LCS();
~LCS();
void ProRun(); //只做动态规划部分的双重循环
void Running(); //供main()调用
void PrintResult(int ,int); //递归输出
};
[cpp]
#include "LCS.h"
#include <iostream>
#include <fstream>
using namespace std;
LCS::LCS()
{
sX = "ABCBDAB";
sY = "BDCABA";
m = sX.size();
n = sY.size();
c = new int *[m+1]; //书中是把字符所在的序号看成了下标,所以得多开辟一个空间
b = new int *[m+1]; //而且在双重循环时会用到一个空的c[0][0]和b[0][0]
for (int i = 0; i <= m; i++)
{
c[i] = new int[n+1];
b[i] = new int[n+1];
}
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= n; j++)
{
c[i][j] = 0; //先赋值
b[i][j] = 0;
}
}
}
LCS::~LCS()
{
for (int i = 0; i <= m; i++)
{
delete c[i]; //释放空间
delete b[i];
}
delete c;
delete b;
}
void LCS::ProRun()
{
//这个算法时间复杂度为O(mn)
for (int i = 1; i<= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (sX[i-1] == sY[j-1])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = LEFTOVER;
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = OVER;
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = LEFT;
}
}
}
}
void LCS::PrintResult(int i, int j)
{
if (i ==0 || j == 0)
{
return;
}
if (b[i][j] == LEFTOVER)
{
PrintResult(i-1,j-1);
cout<<sX[i-1]<<endl;
}
else if (b[i][j] == OVER)
{
PrintResult(i-1, j);
}
else
{
PrintResult(i, j-1);
}
}
void LCS::Running()
{
LCS::ProRun();
LCS::PrintResult(m,n);
}
[cpp]
#include <iostream>
#include "ALSPro.h"
#include "LCS.h"
using namespace std;
void main()
{
//ASL as;
//as.PrintResult();
LCS ls;
ls.Running();
}
补充:软件开发 , C++ ,