基于遗传算法自动组卷的实现

1 遗传算法介绍

1.1　遗传算法概要

遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，它是用来解决多约束条件下的最优问题。

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，它决定了个体的形状的外部表现。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，往往进行简化，如二进制编码，初始种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小挑选个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

遗传算法提供了一种求解复杂系统优化问题的通用框架。它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于很多学科。遗传算法的主要应用领域有：函数优化、组合优化、生产调度问题、自动控制、机器人自动控制、图像处理和模式识别、人工生命、遗传程序设计、机器学习。

1.2　遗传算法的基本操作

遗传算法有三个基本操作：选择、交叉、变异。这些操作又有不同的方法来实现。

（1）选择。选择是用来确定重组或交叉的个体，以及被选个体将产生多少子个体。首选计算适应度：按比例的适应度计算；基于排序的适应度计算。适应度计算之后是实际的选择，按照适应度进行父代个体的选择。可以挑选以下算法：轮盘赌选择、随机遍历抽样、局部选择、截断选择、锦标赛选择。

（2）交叉。基因重组是结合来自父代交配种群中的信息产生新的个体。依据个体编码表示方法的不同，可以有以下的算法：实值重组；离散重组；中间重组；线性重组；扩展线性重组。二进制交叉、单点交叉、多点交叉、均匀交叉、洗牌交叉、缩小代理交叉。

（3）变异。交叉之后子代经历的变异，实际上是子代基因按小概率扰动产生的变化。依据个体编码表示方法的不同，可以有以下的算法：实值变异、二进制变异。

2 自动组卷的实现

自动组卷是根据用户给定的约束条件（总时间、难度系数、考试时间、考试章节、题型比例等），搜索试题库中与特征参数相匹配的试题，从而抽取最优的试题组合。由此可见，自动组卷问题是一个具有多重约束的组合优化问题。

传统的遗传算法存在搜索后期效率低和易形成末成熟收敛的情况。根据具体情况和需求分析要求，对遗传算法进了稍微改进，表现为采用实数编码、分段交叉、有条件生成初始种群。具体解决方案如下。

2.1　染色体编码及初始群体的设计

用遗传算法求解问题，首先要将问题的解空间映射成一组代码串，即染色体的编码问题。在传统的遗传算法中采用二进制编码。用二进制编码时，题库里的每一道题都要出现在这个二进制位串中，1表示该题选中，0表示该题未被选中。这样的二进制位串较长，且在进行交叉和变异遗传算子操作时，各种题型的题目数量不好控制。采用实数编码方案，将一份试卷映射为一个染色体，组成该试卷的每道题的题号作为基因，基因的值直接用试题号表示，每种题型的题号放在一起，按题型分段，在随后的遗传算子操作时也按段进行，保证了每种题型的题目总数不变。比如，要组一份《C语言程序设计》试卷，其选择题5道，填空题5道，简答题3道，则染色体编码是：

(10、76、23、52、101 | 52、36、67、11、123 | 99、85、45)

选择题填空题简答题

试卷初始种群不是采用完全随机的方法产生，而是根据题型比例、总分、答题时间、知识点不重复、不考章节等要求随机产生，使得初始种群一开始就满足了题型、总分、答题时间和知识点等要求。这样加快遗传算法的收敛并减少迭代次数，由于不同的题型是从不同的题型表中取出，有可能在同一个基因串中会出现相同的试题编号，因它们属于不同题型，故这种情况是正常的，不影响组卷。采用分组实数编码，可以克服以往采用二进制编码搜索空间过大和编码长度过长的缺点，同时取消了个体的解码时间，提高了求解速度。

2.2　适应度函数的设计

适应度函数是用来评判试卷群体中个体的优劣程度的指标，遗传算法利用适应度值这一信息来指导搜索方向，而不需要适应度函数连续或可导以及其它辅助信息。因为时间、章节等要求在初始化种群时已经考虑，这里只剩下难度系数要考虑的了。所以适应度函数由试卷难度系数公式转换而成。试卷难度系数公式：P=∑Di×Si/∑Si；其中i=1，2，....N，N是试卷所含的题目数，Ｄi，Ｓi分别是第i题的难度系数和分数。用户的期望难度系数EP与试卷难度系数P之差f越小越好，f=|EP-P|，而适应度函数是值越大越好，因此将目标函数f转换成适应度函数F=e-0.03f，这种采用加权误差的适应度函数可以较好地反映求解组卷问题的特征，当试卷个体对各项组卷约束条件的误差越小时，它的适应度函数值就越大，则表示试卷个体越接近卷目标。

2.3　遗传算子的设计

（1）选择算子。选择算子的作用在于根据个体的优劣程度决定它在下一代是被淘汰还是被复制。通过选择，将使适应度高的个体有较大的生存机会。本系统采用轮盘赌方法，它是目前遗传算法中最常用也是最经典的选择方法。其具体实现为：规模为M的群体P={a1、a2、… am} ，其被选择概率为：（2）交叉算子。由于在编码时采用的是分段实数编码，所以在进行交叉时采用分段单点交叉（按题型分段来进行交叉），整个染色体就表现为多点交叉。交叉的实现过程：将群体中的染色体任意进行两两配对，对每对染色体产生一个[0， 1 ]的随机数r，若r≤pc（据经验，pc值取0.6到0.8），则分段随机产生一个交叉点，然后分段进行互换以得到下一代。

交叉后生成的子代有可能因存在重复的题号而非法。出现这种情况要将出现的题号换成该段中没有出现过的题号，这样重新得到新子代。

（3）变异算子。在遗传算法中，变异概率一般较小。这里不分段进行变异，而是只对某段上的某个基因进行变异。对某个染色体，随机生成一个[0，1]范围内的实数r，若r≤pm（据经验，pm值取0.01到0.02），则对该染色体进行变异，否则不进行变异。变异的操作如下：在[1，n]范围内随机生成一个段号f，设该段的段长为L，则在[1，L]范围内随机生成一个变异位置P，以一定的原则从题库中选择一个变异基因，变异基因的选择原则为：与原基因题型相同的；满足答题时间相同；考试章节相同等要求。

2.4　算法的实现伪代码及实施流程图

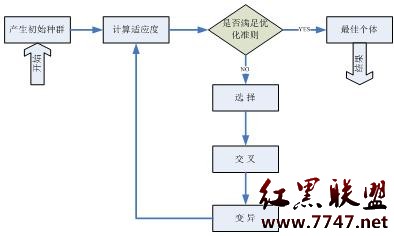
确定参数：最大代数Max，群体规模N，交叉概率pc，变异概率pm，输入用户的组卷要求。算法实施流程如图1所示。

图1 算法实施流程图

2.5　界面设计与实现结果

系统试题库是C 语言试题。试题库中现有单选题、填空题、判断题、程序设计题、简答题等。群体规模设为20，算法执行的最大迭代次数设为200，交叉概率Pc设为0.7，变异概率Pm 设为0.015。

组卷的具体要求：试卷总分100，用时120min，试卷难度系数0.6，不考章节1.2。组卷结果表明，在进化到120代左右时即可生成一份满意的试卷且误差比较小，改进的遗传算法降低了组卷问题的求解难度，组卷效率高、成功率高；且算法对初值不敏感，具有较好的鲁棒性。在初始试卷生成之后，对有必考题要求，可以在试卷生成界面添加必考题。3 结束语

本文利用遗传算法研究了实动自动组卷。实践的结果表明，在满足约束条件的同时，该方法能较快地组成一份试卷。同时，遗传算法在其它方面的应用，值得继续研究、应用

补充：综合编程 , 其他综合 ,