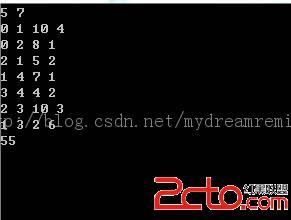
最小费用最大流

<span style="font-size:18px">/* 
    每次找出最短路径（该路径的单位费用和最小）记录该路径（next数组） 
    直到找不出这样一条路径(实际上是没有到达终点的路，因为图中的路是会不停的变动)。我们这里的是Distance[0]>=MAX 

*/  
  
#include<iostream>  
using namespace std;  
#define MAX 1024  
  
int nodes,edges;//节点数和边数  
int capacity[MAX][MAX];//节点之间的流量  
int cost[MAX][MAX];//节点之间的单位费用  
  
int minCost=0;//统计最小费用  
int next[MAX];//为了记录最短路径  
  
int Distance[MAX];//表示每个节点到终点的费用  
inline int min(int a,int b)  
{  
    return a<b?a:b;  
}  
void resetThePath()//找出最短路径,这里还需优化。  
{  
    int i,j;  
    for(i=0;i<nodes-1;i++)  
        Distance[i]=MAX;  
    Distance[nodes-1]=0;  
    next[nodes-1]=-1;  
      
    for(i=nodes-1;i>=0;i--)  
    {  
        for(j=0;j<nodes;j++)  
        {  
            if(cost[j][i]!=MAX)  
            {  
                if(Distance[j]>(Distance[i]+cost[j][i]))  
                {  
                    Distance[j]=Distance[i]+cost[j][i];  
                    next[j]=i;  
                }  
            }  
        }     
    }  
  
    for(i=nodes-1;i>=0;i--)  
    {  
        for(j=0;j<nodes;j++)  
        {  
            if(cost[j][i]!=MAX)  
            {  
                if(Distance[j]>(Distance[i]+cost[j][i]))  
                {  
                    Distance[j]=Distance[i]+cost[j][i];  
                    next[j]=i;  
                }  
        }     
    }     
}  
  
void minCostMaxFlow()  
{  
    while(1)  
    {  
        int i;  
        resetThePath();  
        if(Distance[0]>=MAX)//没有最短路径  
            break;  
        int increase=MAX;//本次最短路径中的流量  
        for(i=0;next[i]!=-1;i=next[i])  
        {  
            increase=min(increase,capacity[i][next[i]]);  
        }  
        for(i=0;next[i]!=-1;i=next[i])//改变图的路径信息  
        {  
            capacity[i][next[i]]-=increase;  
            capacity[next[i]][i]+=increase;  
            if(cost[next[i]][i]==MAX)  
                cost[next[i]][i]=cost[i][next[i]]*(-1);  
            if(!capacity[i][next[i]])  
                cost[i][next[i]]=MAX;  
        }  
        minCost+=Distance[0]*increase;  
    }         
}  
  
void main()  
{  
    while(1)  
    {  
        cin>>nodes>>edges;  
        int i,j;  
        for(i=0;i<nodes;i++)  
        {  
            for(j=0;j<nodes;j++)  
                capacity[i][j]=0;  
            for(j=0;j<nodes;j++)  
                cost[i][j]=MAX;  
        }  
        int firstnode,secondnode,capa,cos;  
        for(i=0;i<edges;i++)  
        {  
            cin>>firstnode>>secondnode>>capa>>cos;  
            capacity[firstnode][secondnode]=capa;  
            cost[firstnode][secondnode]=cos;  
        }  
        minCostMaxFlow();  
        cout<<minCost<<endl;  
    }  
}</span>