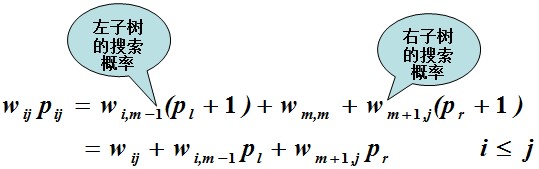hdu1521-排列组合

 

G（x) = ( 1 + x / 1!  + (x^2)/(2!) + .....+ (x ^ n1 ) / （n1!)  ) * （( 1 + x / 1!  + (x^2)/(2!) + .....+ (x ^ n２ ) / （n２!)*.............*(( 1 + x / 1!  + (x^2)/(2!) + .....+ (x ^ nk) / （nk!)  )  

 

求x^m的系数转换成temp / （ m ! )  ;

 

然后求解时，temp * （m! ) 就是x ^ m的系数

 

#include<map>  
#include<set>  
#include<list>  
#include<cmath>  
#include<ctime>  
#include<deque>  
#include<stack>  
#include<bitset>  
#include<cstdio>  
#include<vector>  
#include<cstdlib>  
#include<cstring>  
#include<iomanip>  
#include<numeric>  
#include<sstream>  
#include<utility>  
#include<iostream>  
#include<algorithm>  
#include<functional>  
  
using namespace std ;  
  
double fac[ ] = { 1 , 1 , 2 , 6 , 24 , 120 , 720 , 5040 , 40320 , 362880 , 3628800 , 39916800 } ;  
  
int main()  
{  
    int n , m ;  
    double a[ 11 ] , b[ 11 ] , num1[ 11 ], num2[ 11 ];  
    while( scanf( "%d%d" , &n , &m ) != EOF )  
    {  
        for( int i = 0 ; i < n ; ++i )  
        {  
            scanf( "%lf" , &a[ i ] ) ;  
        }  
        for( int i = 0 ; i <= m ; ++i )  
            num1[ i ] = num2[ i ] = 0.0 ;  
        for( int i = 0 ; i <= a[ 0 ] ; ++i )  
        {  
            num1[ i ] = 1.0 / fac[ i ] ;  
        }  
        for( int i = 1 ; i < n ; ++i )  
        {  
            for( int j = 0 ; j <= m ; ++j )  
            {  
                for( int k = 0 ; k <= a[ i ] && k + j <= m ; ++k )  
                {  
                    num2[ k + j ] += ( num1[ j ] / fac[ k ] ) ;  
                }  
            }  
            for( int j = 0 ; j <= m ; ++j )  
            {  
                num1[ j ] = num2[ j ] ;  
                num2[ j ] = 0 ;   
            }  
        }  
        printf( "%.lf\n" , num1[ m ] * fac[ m ] ) ;  
    }  
    return 0;  
}  

 

补充：软件开发 , C++ ,