poj - 3321 - Apple Tree


		题意：一棵苹果树有n个结点，开始时每个结点有一个苹果，这n个结点由m条枝连起来，现执行以下两种操作，C x：如果结点x原来有苹果，则把它摘掉，如果没有，则长出1个苹果。Q x：询问以x为根的树的苹果共几个？
 
 
——>>这题转换是关键！要求以x为根的树的苹果共几个，如果能够转换为求一个数组a的[L, R]上的连续和，那就可以用ST或者BIT了。事实证明，确实可以做到这种转换。
 
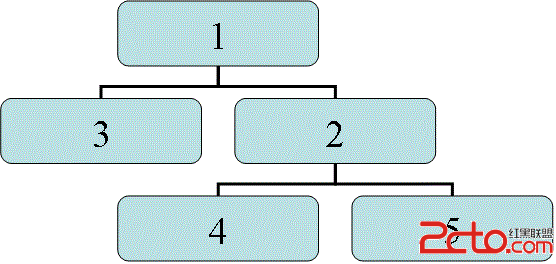
例如：原来的树如下：如果询问2，那么共有2、4、5这3个苹果，但2、4、5不是连续的呀？？？
 

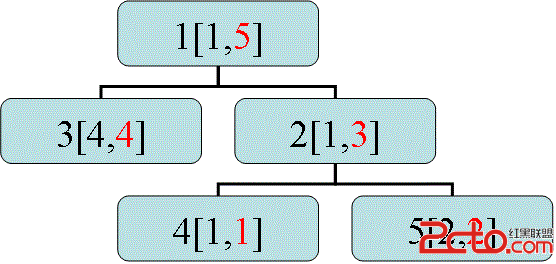
得用dfs转换后如下：[L, R]，其中所有的L存于L数组中，所有的R存于R数组中，R为新编号。
 

如果询问2，也就是求数组a在[1, 3]上的连续和。利用BIT或者ST就可解决TLE的问题啦。
 
（知道这样做可以省时间，但也很容易TLE的，我用上ST，TLE了几次，改用树状数组，TLE了十余次，最后，将那个vector<int>G[maxn]改为typedefvector<int> INT;
 
vector<INT>G(maxn);竟然奇迹般地AC!了什么情况，这是……）
[cpp] 
#include <iostream>  
#include <cstdio>  
#include <vector>  
#include <cstring>  
  
using namespace std;  
  
const int maxn = 100000 + 10;       //N ≤ 100,000,M ≤ 100,000  
int lowerbit[maxn], C[maxn], L[maxn], R[maxn], dfs_clock = 1, N;  
bool vis[maxn], a[maxn];  
typedef vector<int> INT;  
vector<INT> G(maxn);  
  
void dfs(int x)     //对苹果树进行重新编号  
{  
    vis[x] = 1;     //标记为已访问  
    L[x] = dfs_clock;       //dfs_clock为计数器  
    for(unsigned int i = 0; i < G[x].size(); i++)       //对所有相邻结点进行检查  
    {  
        int v = G[x][i];  
        if(!vis[v]) dfs(v);     //如果没访问过，访问  
    }  
    R[x] = dfs_clock++;     //新编号在这里！  
}  
void update(int x)      //BIT更新函数  
{  
    int val;  
    if(a[x]) val = -1;  
    else val = 1;  
    a[x] = !a[x];       //该结点取反即可  
    while(x <= N)  
    {  
        C[x] += val;  
        x += lowerbit[x];  
    }  
}  
int sum(int x)      //BIT求数组a的前x项和  
{  
    int ret = 0;  
    while(x > 0)  
    {  
        ret += C[x];  
        x -= lowerbit[x];  
    }  
    return ret;  
}  
int main()  
{  
    int M, i, u, v;  
    scanf("%d", &N);  
    for(i = 1; i <= N; i++)     //初始化  
    {  
        C[i] = i&(-i);      //C为BIT结点的连续和  
        a[i] = true;  
        lowerbit[i] = i&(-i);     //lowerbit为二进制表达式中最右边的1所对应的值,这里，用i&(-i)比用C[i]直接赋值要快！  
    }  
    for(i = 0; i < N-1; i++)  
    {  
        scanf("%d%d", &u, &v);  
        G[u].push_back(v);      //测试证明，不需要考虑双向  
    }  
    dfs(1);  
    scanf("%d", &M);  
    char ch;  
    for(i = 0; i < M; i++)  
    {  
        getchar();  
        scanf("%c%d", &ch, &v);  
        if(ch == 'Q') printf("%d\n", sum(R[v])-sum(L[v]-1));        //经测试，先判断为'Q'用的时间更少  
        else update(R[v]);  
    }  
    return 0;  
}

补充：软件开发 , C++ ,