poj 2762 Going from u to v or from v to u (Kosaraju+缩点+单链图)

题目链接: poj 2762

题目大意: 给定有向图，问是否满足对于任意的顶点X和Y

使得X->Y或Y->X至少存在一条路径

解题思路: 联通分量找出，缩成点形成DAG(有向无环图)

使得缩点后的图满足题意，必须是单链图

换句话说同一个点只能有一个分支

有两个分支的话，分支之间是不能到达的

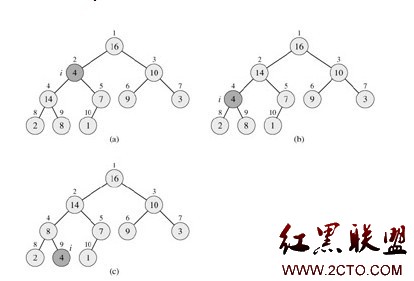
图1橙色顶点无法到达绿色还有另一橙色分支

而图2的绿色顶点都可以到达

判断单链图：缩点后有C块联通分量，则有1个入度0出度1，1个入度1出度 0，C-2个入度1出度1顶点

代码:

//Final    kosaraju+缩点+单链图  
#include <stdio.h>  
#include <string.h>  
#include <stdlib.h>  
#define MAX 1010  
struct snode{  
    int to,next;  
}edge1[MAX*12],edge2[MAX*12],edge3[MAX*12];  
int visit1[MAX],In[MAX],To[MAX],pre1[MAX],pre2[MAX],Index1,Index2,len,k,list[MAX];  
int father[MAX],pre3[MAX],Index3;  
  
void Add_edge1(int a,int b)  //建立正向图  
{  
    edge1[Index1].to=b,edge1[Index1].next=pre1[a];  
    pre1[a]=Index1++;  
}  
  
void Add_edge2(int a,int b)  //建立逆向图  
{  
    edge2[Index2].to=b,edge2[Index2].next=pre2[a];  
    pre2[a]=Index2++;  
}  
  
void Kosaraju(int u)     //第一次正向搜索  
{  
    int i,v;  
    for(i=pre1[u];i!=-1;i=edge1[i].next)  
    {  
        v=edge1[i].to;  
        if(visit1[v]==0)  
        {  
            visit1[v]=1;  
            Kosaraju(v);  
        }  
    }  
    list[k++]=u;  
}  
  
void DFS(int u,int Father)  //第二次是分块逆向搜索，搜索点的顺序与正向一样  
{  
    int i,v;  
    visit1[u]=2;  
    father[u]=Father;  
    for(i=pre2[u];i!=-1;i=edge2[i].next)  
    {  
        v=edge2[i].to;  
        if(visit1[v]==1)  
            DFS(v,Father);  
    }  
}  
  
void Add_edge3(int a,int b)   //建立缩点后的图  
{  
    int i;  
    if(a==b)  
        return ;  
    for(i=pre3[a];i!=-1;i=edge3[i].next)   //如果有重边则不加入  
    {  
        if(edge3[i].to==b)  
            return ;  
    }  
    In[b]++; To[a]++;  
    edge3[Index3].to=b,edge3[Index3].next=pre3[a];  
    pre3[a]=Index3++;  
}  
  
int main()  
{  
    int t,n,m,i,j,a,b,c,v,k1,k2,k3,pd;  
    scanf("%d",&t);  
    while(t--)  
    {  
        scanf("%d%d",&n,&m);  
          
        Index1=Index2=Index3=0;  
        memset(In,0,sizeof(In));  
        memset(To,0,sizeof(To));  
        memset(pre1,-1,sizeof(pre1));  //正向图  
        memset(pre2,-1,sizeof(pre2));  //逆向图  
        memset(pre3,-1,sizeof(pre3));  //缩点后的图  
        memset(visit1,0,sizeof(visit1));  
        memset(father,0,sizeof(father));  
        for(i=0;i<m;i++)  
        {  
            scanf("%d%d",&a,&b);  
            Add_edge1(a,b);  
            Add_edge2(b,a);  
        }  
        if(m<n-1)     //边数小于顶点数-1不能构成图或者树  
        {  
            printf("No\n");  
            continue;  
        }  
        for(i=1,k=0;i<=n;i++)  
        {  
            if(!visit1[i])  
            {  
                visit1[i]=1;  
                Kosaraju(i);  
  
            }  
        }     
        for(j=k-1,c=0;j>=0;j--)  
        {  
            if(visit1[list[j]]==1)  
            {  
                DFS(list[j],++c);  
            }  
        }  
        for(i=1;i<=n;i++)  
        {  
            for(j=pre1[i];j!=-1;j=edge1[j].next)  
            {  
                v=edge1[j].to;        
                Add_edge3(father[i],father[v]);  
            }  
        }  
        if(c==1)  
        {  
            printf("Yes\n");  
            continue;  
        }  
        for(i=1,k1=k2=k3=pd=0;i<=c;i++)  //缩点后的图是否为单链的树  
        {  
            if(In[i]==1&&To[i]==0)   //有一个终点  
            {  
                k1++;  
                continue;  
            }  
            if(In[i]==0&&To[i]==1)   //有一个起点  
            {  
                k2++;  
                continue;  
            }  
            if(In[i]==1&&To[i]==1)   //有c-2个中间点  
            {  
                k3++;  
                continue;  
            }  
        }  
        pd=k1+k2+k3;  
        if(k1==1&&k2==1&&pd==c)  
            printf("Yes\n");  
        else  
            printf("No\n");  
    }  
    return 0;

补充：软件开发 , C++ ,