hdu 4756 Install Air Conditioning（2013南京网络赛）

题意就是求MST中删去一条边后，次小生成树最大的那颗。注意题中说了“ there are so many wires between two specific dormitories” 。也就是说与0节点（power plant）相连的MST边是不会出故障的，所以要特殊考虑一下所有MST边都跟0节点相连的情况。

删除MST中某条边后的次小生成树用树形dp解决，传送门

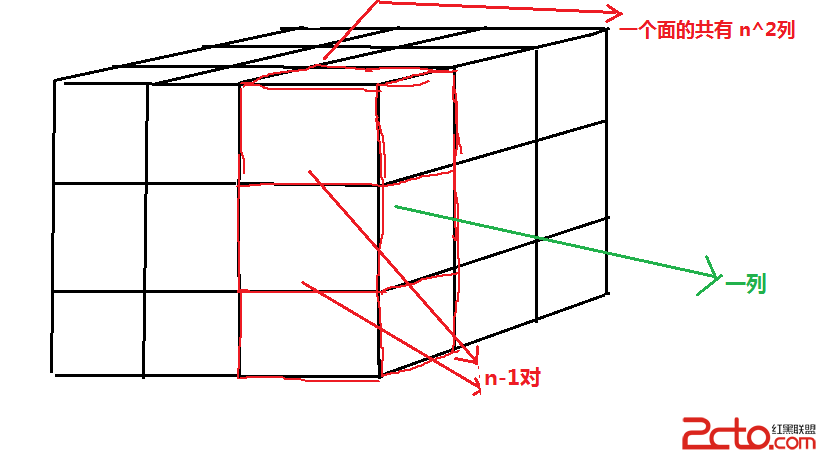
我的理解是：删除MST边<u, v>之后， MST被划分成u跟v两个子树，新添加的非MST边必然是连接u跟v两颗子树的原图中的非MST边，这可以用dfs解决。dp[u][v]代表两颗子树的最短距离，用每个点p的非MST边g[p][i]去更新所有的dp[u][v]，时间复杂度O(n^2)。

//#pragma comment(linker, "/STACK:1024000000,1024000000")  
#include<algorithm>  
#include<iostream>  
#include<cstring>  
#include<fstream>  
#include<sstream>  
#include<vector>  
#include<string>  
#include<cstdio>  
#include<bitset>  
#include<queue>  
#include<stack>  
#include<cmath>  
#include<map>  
#include<set>  
#define FF(i, a, b) for(int i=a; i<b; i++)  
#define FD(i, a, b) for(int i=a; i>=b; i--)  
#define REP(i, n) for(int i=0; i<n; i++)  
#define CLR(a, b) memset(a, b, sizeof(a))  
#define debug puts("**debug**")  
#define LL long long  
#define PB push_back  
#define MP make_pair  
#define eps 1e-10  
using namespace std;  
  
const int maxn = 1010;  
const double INF = 1e20;  
int n, T, fa[maxn];  
double mst, k, x[maxn], y[maxn], g[maxn][maxn], dp[maxn][maxn], d[maxn];  
bool vis[maxn];  
vector<int> G[maxn];  
  
template <class T> T sqr(T x) { return x*x; }  
double dist(int i, int j)  
{  
    return sqrt(sqr(x[i]-x[j]) + sqr(y[i] - y[j]));  
}  
  
void read()  
{  
    scanf("%d%lf", &n, &k);  
    REP(i, n) scanf("%lf%lf", &x[i], &y[i]);  
    REP(i, n)  
    {  
        FF(j, i+1, n) g[i][j] = g[j][i] = dist(i, j), dp[i][j] = dp[j][i] = INF;  
        g[i][i] = INF;  
        vis[i] = 0;  
        fa[i] = 0;  
        G[i].clear();  
    }  
}  
  
void prim()  
{  
    REP(i, n) d[i] = g[0][i];  
    vis[0] = 1;  
    fa[0] = -1;  
    d[0] = INF;  
    mst = 0;  
    FF(i, 1, n)  
    {  
        int pos = 0;  
        FF(j, 1, n) if(!vis[j] && d[pos] > d[j]) pos = j;  
  
        mst += d[pos];  
        vis[pos] = 1;  
  
        //构造MST  
        G[pos].PB(fa[pos]);  
        G[fa[pos]].PB(pos);  
  
        FF(j, 1, n) if(!vis[j] && g[pos][j] < d[j])  
            d[j] = g[pos][j], fa[j] = pos;  
    }  
}  
  
//用所有非MST边g[p][i] 更新所有dp[u][v]  
double dfs(int p, int u, int f)  
{  
    double ans = INF;  
    REP(i, G[u].size())  
    {  
        int v = G[u][i];  
        if(v != f)  
        {  
            double tmp = dfs(p, v, u);  
            ans = min(ans, tmp);  
            dp[u][v] = dp[v][u] = min(dp[u][v], tmp);  
        }  
    }  
    //保证非MST边才能更新  
    if(p != f) ans = min(ans, g[p][u]);  
    return ans;  
}  
  
double solve()  
{  
    REP(i, n) dfs(i, i, -1); //每个点更新一次  
  
    //MST中所有跟0节点相连的边是不会出问题的  
    bool flag = 0;  
    FF(i, 1, n) if(fa[0] != i && fa[i] != 0) flag = 1;  
    if(!flag) return mst * k;  
  
    double ret = 0;  
    //求MST边删除后的次小生成树的最大值  
    FF(i, 1, n) FF(j, i+1, n) if(fa[i] == j || fa[j] == i)ret = max(ret, dp[i][j] - g[i][j]);  
    return (mst + ret) * k;  
}  
  
int main()  
{  
    scanf("%d", &T);  
    while(T--)  
    {  
        read();  
        prim();  
        printf("%.2lf\n", solve());  
    }  
    return 0;  
}

补充：软件开发 , C++ ,