poj1236-Tarjan算法

题目大意：
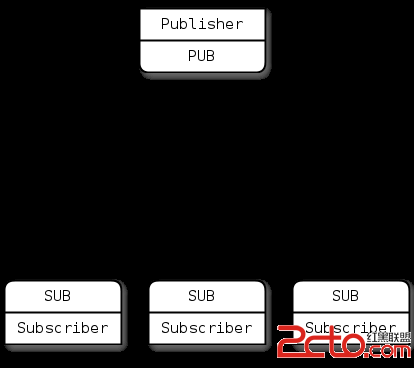
    一些学校连成了网络，在学校之间存在某个协议:每个学校都维护一张传送表，表明他们要负责将收到的软件传送到表中的所有学校。如果A在B的表中，那么B不一定在A的表中。
    现在的任务就是，给出所有学校及他们维护的表，问1、如果所有学校都要被传送到，那么需要几份软件备份；2、如果只用一份软件备份，那么需要添加几条边？
题目解法：
    这道题就是求学校之间连成网络的强联通分量。第一问中软件只要在一个分量中存在一份，那么分量中的其他学校必然也可以拿到这份软件；第二问中要所有学校都连成一个强联通分量，只需要将图中的强联通分量互相之间联通就好了。添加的边数就是缩点后入度为0的点和出度为0的点的最大值（可意会不可言传。。）。
题目源码：关键部分都用注释标明了
[html]
//#define LOCAL
#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;

#define MAXN 110
#define INF 0x3f3f3f3f
int n;
int map[MAXN][MAXN];
int low[MAXN];
int dfn[MAXN];
int stack[MAXN], head;
int instack[MAXN];
int belong[MAXN];
int in[MAXN];
int out[MAXN];
int index, cnt;

int min(int a, int b)
{
    return a < b ? a : b;
}

int max(int a, int b)
{
    return a > b ? a : b;
}

void init()
{
    int i, j;
    int temp;
    memset(map, 0, sizeof(map));
    memset(dfn, -1, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    index = cnt = 1;
    head = 0;
    for(i= 1; i <= n; i++)
    {
        while(scanf("%d", &temp) && temp)
        {
            map[i][temp] = 1;
        }
    }
}

void tarjan(int x)
{
    int i, a;
    low[x] = dfn[x] = index; // 刚搜到一个节点时low = dfn
    index++;
    stack[++head] = x; // 将该节点入栈
    instack[x] = 1; // 将入栈标记设置为1
    for(i = 1; i <= n; i++) // 遍历入栈节点的边
    {
        if(!map[x][i]) // 如果两点之间没有边
            continue; // 不用管它
        if(dfn[i] == -1) // 如果新搜索到的节点是从未被搜索过
        {
            tarjan(i); // 那自然就得搜索这个节点
            low[x] = min(low[x], low[i]); // 回溯的时候改变当前节点的low值
        }
        else if(instack[i]) // 如果新搜索到的节点已经被搜索过而且现在在栈中
        {
            low[x] = min(low[x], dfn[i]); // 更新当前节点的low值，这里的意思是两个节点之间有一条可达边，而前面
        }                                 // 而前面节点已经在栈中，那么后面的节点就可能和前面的节点在一个联通分量中
    }

    if(low[x] == dfn[x]) // 最终退回来的时候 low == dfn ，没有节点能将根节点更新，那
    {                   // low == dfn 的节点必然就是根节点
        int temp;
        while(1) // 一直出栈到此节点，这些元素是一个强联通分量
        {
            temp = stack[head--]; // 弹出栈元素
            belong[temp] = cnt; // 为了方便计算，将强联通分量进行标记
            instack[temp] = 0; // 将栈内标记置为0
            if(temp == x)     // 一直弹到x出现为止
                break;
        }
        cnt++;
    }
}


void solve()
{
    int i, j;
    int t1, t2;
    while(scanf("%d", &n) != EOF) //
    {
        init(); // 初始化
        for(i = 1; i <= n; i++) //
            if(dfn[i] == -1) // 如果某点没被访问过，则对其进行tarjan
                tarjan(i);          // tarjan的成果是得到了一个belong数组，记录每个节点分别属于哪个强联通分量
        for(i = 1; i <= n; i++) // 遍历每条边，找到缩点之后的边
        {
            for(j = 1;j <= n; j++)
            {
                if(map[i][j] && belong[i] != belong[j]) // 两点之间有边，但不是属于一个强联通分量的边
                {
                    out[belong[i]]++; // 缩点后的点入度+1
                    in[belong[j]]++;// 缩点后的点出度+1
                }
            }
    &nbs

补充：软件开发 , C++ ,