Hdu 4281 Judges' response (DP_背包|TSP)

题目大意:给定n个地点的坐标和每个地点的权值，即一张图n个点，点有点权边有边权。现在裁判在点1，需要分配这些裁判到这些点去，已知每个裁判能够到点权之和不大于m，而且一个点不能由两个裁判访问。现在给出两个问题，1、最少几个裁判可以覆盖所有点 2、给定无数个裁判，怎么样访问这些点使得总边权和最小，裁判访问完必须回到1点，而且一个裁判访问的点权之和不能超过m。

解题思路：昨天天津赛区的1004题，比赛的时候都想到了算法，就是不敢去敲，一直在想稳妥的算法，最终没有ac。
    晚一点和其他学校的acmer交流聊到这题，就想着要不要去试下，如果不行的话明天去搜论文，因为这是很经典的mTSP问题。但是没想到竟然ac了，神奇得ac了，坑爹地ac了，复杂度O(2^(2*n)+(2^n*n^2))，排名还很靠前。ac完想到的第一句话不是终于ac而是：尼玛,中山大学就喜欢这么暴力么?..
    有可能不是正解，但还是写下思路，感觉两个问题都很经典。
    第一问：求最少的裁判覆盖这些点，思路是先将2^n种地点的选择集合压缩成2^n个物品，物品的权值为集合内的点权之和，如果总和<=m，那么他是一种合法的组合，存起来。这样就得到tot种合法组合，对这tot种组合进行01背包，dp[i]表示容量为i时的最小费用，和常规的背包不同，但本质是一样的。状态转移方程:dp[i] = min(dp[i],dp[j]+1) (j为i的子集,i = j | state[k]并且j和state[k]没有交集，state[k]表示第k个合法物品)
    PS：后来发现这一问其实用贪心就可以解决，每次都选最大的，直到本次不能选为止，看能选几次.
    第二问：多旅行商问题即mTsp，感觉挺经典的，思路是将mtsp转化成普通的tsp，然后再将各个tsp合并成答案。先要O(2^n*n^2)的预处理得到np[i]表示一个裁判走的集合为i的所有地点又回到最初的点的最少权值和，然后np[i] = min(np[i],np[k|(1<<0)]+np[(i-k)|(1<<0)])(i必须包含0节点，因为子集可能不含0节点，所以要和1<<0或起来，这样才是将两个裁判所走的边权和合并)。

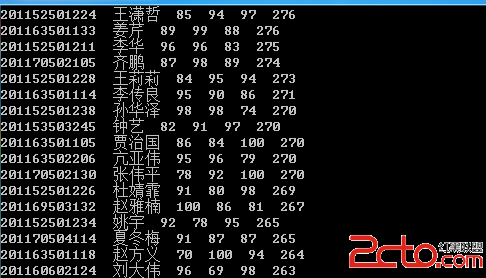
测试数据：
Input:
3 3
0 0
0 3
0 4
0
2
2
3 2
0 0
0 3
1 0
0
1
2
3 1
0 0
0 3
0 1
0
1
2
4 9
1 2
1 3
2 1
3 1
0
5
6
4
16 3500
30 40
37 52
49 49
52 64
31 62
52 33
42 41
52 41
57 58
62 42
42 57
27 68
43 67
58 48
58 27
37 69
0
19
30
16
23
11
31
15
28
8
8
7
14
6
19
11

Input:
2 14
2 8
-1 -1
2 11
1 164

代码：
[cpp]
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define MIN (1<<17)
#define MAX 110000
#define INF (1<<29)
#define min(a,b) ((a)<(b)?(a):(b))

int tot, ans1, ans2, n, m; //总合法物品数，第一、第二问答案
int x[20], y[20], val[20]; //左边和点权
int dp[MAX], state[MIN]; //第一问用到
int map[20][20], isok[MIN]; //边权、合法物品集合
int cost[17][MIN], np[MIN]; //第二问用到

void Initial() {

    int i, j, k;

    tot = 0;
    memset(map, 0, sizeof (map));
    for (i = 0; i < (1 << n); ++i)
        dp[i] = np[i] = INF;
    for (i = 0; i <= n; ++i)
        for (j = 0; j < (1 << n); ++j)
            cost[i][j] = INF;
    cost[0][1] = 0;
}

int cmp1(int a, int b) {

    return a > b;
}

int Solve_Tanxin() {

    int i, j, k, mmin = INF;
    int tp[20], vis[20];

    for (i = 0; i < n; ++i)
        vis[i] = 0, tp[i] = val[i];
    sort(tp, tp + n, cmp1);
    for (i = 1; i <= n; ++i) {

        int rest = m;
        for (j = 0; j < n; ++j)
            if (!vis[j] && tp[j] <= rest)
                rest -= tp[j], vis[j] = 1;
        ;
        for (j = 0; j < n && vis[j] == 1; ++j);
        if (j == n) return i;
    }
    return INF;
}

int Solve_First() {

    int i, j, k, mmin = INF;

    dp[0] = 0;
    for (i = 0; i < tot; ++i)
        for (j = (1 << n) - 1; j >= 0; --j) {

            if (dp[j] == INF) continue;
            int st = j + state[i];
            if (st != (j | state[i])) continue;
            dp[st] = min(dp[st], dp[j] + 1);
        }

    return dp[(1 << n) - 1];
}

void GetDist() {

    for (int i = 0; i < n; ++i)
        for (int j = i + 1; j < n; ++j) {

            double xx = x[i] - x[j];
            double yy = y[i] - y[j];
            xx *= xx, yy *= yy;
            map[i][j] = map[j][i] = ceil(sqrt(xx + yy));
        }
}

int ok(int x) {

    int sum = 0, i;
    for (i = 0; i < n; ++i)
        if (x & (1 << i)) sum += val[i];
    return sum <= m;
}

int TSP_Second() {

    int i, j, k;

    GetDist();
    for (i = 1; i < (1 << n); ++i) if (isok[i]) {

            for (j = 0; j < n; ++j) if (i & (1 << j)) {

                    np[i] = min(np[i], cost[j][i] + map[j][0]);
                    for (k = 0; k < n; ++k) if ((i & (1 << k)) == 0)
           &

补充：软件开发 , C++ ,