HDU 1428 漫步校园(记忆化搜索)

Problem Description
LL最近沉迷于AC不能自拔，每天寝室、机房两点一线。由于长时间坐在电脑边，缺乏运动。他决定充分利用每次从寝室到机房的时间，在校园里散散步。整个HDU校园呈方形布局，可划分为n*n个小方格，代表各个区域。例如LL居住的18号宿舍位于校园的西北角，即方格(1,1)代表的地方，而机房所在的第三实验楼处于东南端的(n,n)。因有多条路线可以选择，LL希望每次的散步路线都不一样。另外，他考虑从A区域到B区域仅当存在一条从B到机房的路线比任何一条从A到机房的路线更近(否则可能永远都到不了机房了…)。现在他想知道的是，所有满足要求的路线一共有多少条。你能告诉他吗?

Input
每组测试数据的第一行为n(2=<n<=50)，接下来的n行每行有n个数，代表经过每个区域所花的时间t(0<t<=50)(由于寝室与机房均在三楼，故起点与终点也得费时)。

Output
针对每组测试数据，输出总的路线数(小于2^63)。

Sample Input
3
1 2 3
1 2 3
1 2 3
3
1 1 1
1 1 1
1 1 1

Sample Output
1
6
******************************************************************************************************************************

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1428

题目要求问左上角走到右下角有多少条路，要求如题目描述的A区域到B区域最短距离。题目主要地方已在上面描红。

方法：记忆化搜索(BFS+DFS+状态记录)

代码：
[cpp]
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define LL __int64

using namespace std;

LL n,tot;
LL Map[55][55],vis[55][55];//图，每一点的状态(有多少条路)
LL dis[55][55];//终点到各点的最短距离
LL dir[][2]={{0,-1},{-1,0},{1,0},{0,1}};//方向

struct Node{
    int x,y,step;
};

queue<Node>que;//队列

void bfs(){//宽搜，确定终点到各点距离
    Node now,next;
    int i,j;
    now.x=n,now.y=n,now.step=0,tot=0;
    que.push(now);
    dis[n][n]=Map[n][n];
    while(!que.empty()){
        now=que.front(),que.pop();
        for(i=0;i<4;i++){
            next.x=now.x+dir[i][0],next.y=now.y+dir[i][1],next.step=now.step+1;
            if(next.x<1||next.y<1||next.x>n||next.y>n) continue;
            if(dis[next.x][next.y]>dis[now.x][now.y]+Map[next.x][next.y]||dis[next.x][next.y]==-1){
                dis[next.x][next.y]=dis[now.x][now.y]+Map[next.x][next.y];
                que.push(next);
            }
        }
    }
}

LL dfs(LL x,LL y){//深搜，确定有多少条路可到达
    int sx,sy,i;
    if(vis[x][y]) return vis[x][y];//路已经走过，返回这点已经有的值(记忆化搜索)
    if(x==n&&y==n){//能够到达终点，多一条路，return 1;
        return 1;
    }
    for(i=0;i<4;i++){
        sx=x+dir[i][0],sy=y+dir[i][1];
        if(sx>n||sy>n||sx<1||sy<1) continue;
        if(dis[sx][sy]>=dis[x][y]) continue;//题目要求选短的路
        vis[x][y]+=dfs(sx,sy);
    }
    return vis[x][y];
}
//主函数
int main(){
    LL i,j;
    while(~scanf("%I64d",&n)){
        for(i=1;i<=n;i++)
        for(j=1;j<=n;j++) scanf("%I64d",&Map[i][j]);
        memset(dis,-1,sizeof(dis));
        memset(vis,0,sizeof(vis));
        bfs();
        dfs(1,1);
        printf("%I64d\n",vis[1][1]);//记忆化搜索，从终点返回，所以是vis[1][1]
    }
    return 0;
}

特别地，记忆化搜索在什么地方体现出来呢，
在DFS中，如果把DFS不使用记忆化搜索而改成如下代码(普通深搜)：
[cpp]
void dfs(int x,int y){
    int sx,sy,i;
    if(x==n&&y==n){
        tot++;//tot记录能够到达终点的路的条数
        return;
    }
    for(i=2;i<4;i++){
        sx=x+dir[i][0],sy=y+dir[i][1];
        if(sx>n||sy>n) continue;
        if(dis[sx][sy]>=dis[x][y]) continue;
        dfs(sx,sy);
    }
}

这样伱就挂了！！TLE，MLE。

再看一张图，苊对记忆化搜索的最基础的理解：

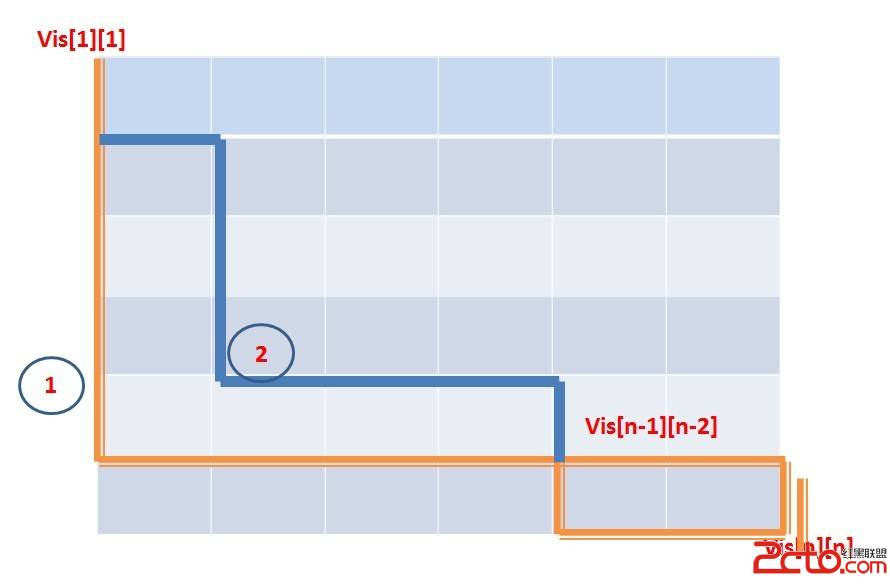
深搜的时候是从vis[1][1]开始搜的，第一次直搜到vis[n][n]，然后返回的时候可以得到vis[n-1][n-2]那个点的路,当第二次搜到vi[n-1][n-2]这个点的时候就不用往下搜了，直接加上在这个点的路，OK，节约时间。
作者：madrishing

补充：软件开发 , C++ ,