UVA 270 (13.11.06)

 

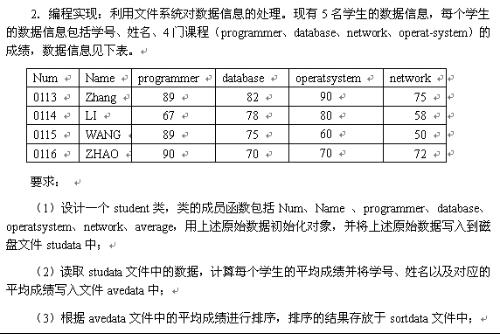
 Lining Up 

``How am I ever going to solve this problem?" said the pilot.

Indeed, the pilot was not facing an easy task. She had to drop packages at specific points scattered in a dangerous area. Furthermore, the pilot could only fly over the area once in a straight line, and she had to fly over as many points as possible. All points were given by means of integer coordinates in a two-dimensional space. The pilot wanted to know the largest number of points from the given set that all lie on one line. Can you write a program that calculates this number?

Your program has to be efficient!

Input

The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.

The input consists of N pairs of integers, where 1 < N < 700. Each pair of integers is separated by one blank and ended by a new-line character. The list of pairs is ended with an end-of-file character. No pair will occur twice.

Output

For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.

The output consists of one integer representing the largest number of points that all lie on one line.

Sample Input

1

 

1 1

2 2

3 3

9 10

10 11

Sample Output

3

 

题意：有一个飞行员，执行任务时只能沿一条直线飞行，他需要沿某条直线飞行时，经过的点最多，输出点数最大值。点对最多700对，时间限制3秒。

做法：其实就是求共线点最多的值啦，做法是采取一个结构体储存坐标，然后设置一个数组，储存每个点与其他剩下的点的斜率各是多少，斜率一样就表明再一条线上。

做题过程感悟：题目要求的格式要看清楚，然后逻辑要分好，要采取足够快的算法，不然超时！

 

AC代码：

 

#include<stdio.h>  
#include<string.h>  
#include<algorithm>  
  
using namespace std;  
  
struct Pos {  
    double x;  
    double y;  
} p[707];  
  
int main() {  
    int n;  
    char str[100];  
    scanf("%d", &n);  
    getchar();  
    getchar();  
    while(n--) {  
        int pos1 = 0;  
        double sx[1000];  
  
        while(gets(str) && str[0] != '\0') {  
            sscanf(str, "%lf%lf", &p[pos1].x, &p[pos1].y);  
            pos1++;  
        }  
  
        int max = 0;  
  
        int pos2;  
        double xl[1000];  
        for(int i = 0; i < pos1; i++) {  
            pos2 = 0;  
            for(int j = 0; j < pos1; j++) {  
                if(i != j)  
                    xl[pos2++] = (p[i].y - p[j].y) / (p[i].x - p[j].x);  
            }  
  
            sort(xl, xl+pos2);  
            for(int k1 = 0; k1 < pos2; k1++) {  
                int same = 2;  
                int k2 = k1;  
                for(int k3 = k2+1; xl[k2] == xl[k3]; same++, k2++, k3++);  
                if(same > max)  
                    max = same;  
            }  
        }  
        printf("%d\n",  max);  
        if(n != 0)  
            printf("\n");  
    }  
    return 0;  
}  

 

 

补充：软件开发 , C++ ,