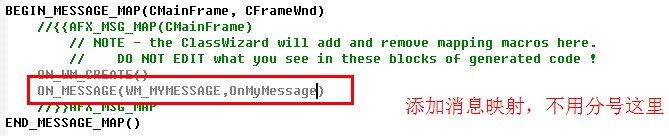
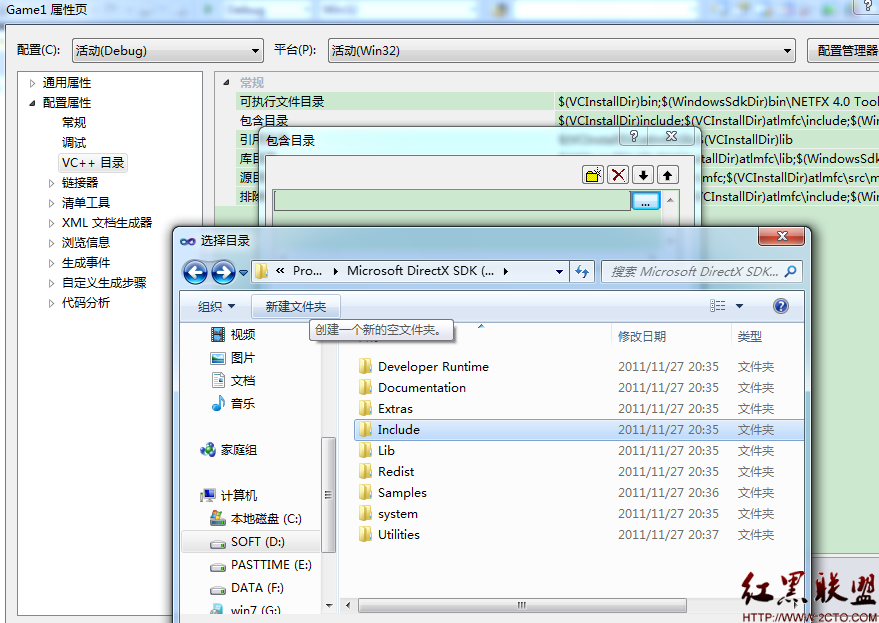
VC++2012编程演练数据结构稀疏矩阵

如果在矩阵中，多数的元素为0，称此矩阵为稀疏矩阵（sparse matrix）。
由于矩阵在程序中常使用二维阵列表示，二维阵列的大小稀疏矩阵与使用的存储器空间成正比，如果多数的元素没有数据，则会造成存储器空间的浪费，为此，必须设计稀疏矩阵的阵列储存方式，利用较少的存储器空间储存完整的矩阵数据。
　　二维数组Amn中有N个非零元素，若N<<m*n（N/m*n<=0.2),则称A为稀疏矩阵。
　　由于稀疏矩阵中含有很多的0元素,在计算机中存储会浪费很多的空间,因此我们通常采用压缩存储的方法。
　稀疏矩阵的计算速度更快,因为M AT L A B只对非零元素进行操作,这是稀疏矩阵的一个突出的优点.
　　假设矩阵A,B中的矩阵一样.计算2*A需要一百万次的浮点运算,而计算2*B只
　　需要2 0 0 0次浮点运算.
　　因为M AT L A B不能自动创建稀疏矩阵,所以要用特殊的命令来得到稀疏矩阵,在下一节
　　中将给出这些命令.前面章节中的算术和逻辑运算都适用于稀疏矩阵.
　　对于一个用二维数组存储的稀疏矩阵Amn,如果假设存储每个数组元素需要L个字节,那么存储整个矩阵需要m*n*L个字节.但是,这些存储空间的大部分存放的是0元素,从而造成大量的空间浪费.为了节省存储空间,可以只存储其中的非0元素.
　　对于矩阵Amn的每个元素aij,知道其行号i和列号j就可以确定其位置.因此对于稀疏矩阵可以用一个结点来存储一个非0元素.该结点可以定义如下:
　　[i,j,aij]
　　该结点由3个域组成,i:行号,j:列号;aij元素值.这样的结点被称为三元组结点.矩阵的每一个元素Qij,由一个三元组结点(i,j,aij)唯一确定.
　　例如稀疏矩阵A:
　　50 0 0 0
　　10 0 20 0
　　0 0 0 0
　　-30 0 -60 5
　　其对应的三元组表为：
　　1 1 50
　　2 1 10
　　2 3 20
　　4 1 -30
　　4 3 -60
　　4 4 5
我们创建一个工程

类的声名如下
[cpp]
#if !defined(AFX_XISHU_H__73B83FF2_CCDD_4354_9761_2BEEE23A0B08__INCLUDED_)
#define AFX_XISHU_H__73B83FF2_CCDD_4354_9761_2BEEE23A0B08__INCLUDED_

#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000

//稀疏矩阵的类定义与操作xishu.h
//假设非0元个数的最大值为100
#define MAXSIZE 100
//三元组顺序表
class TSMatrix;
class Triple
{public:
int ii,jj;//行号和列号
ElemType e;
friend class TSMatrix;
}; www.zzzyk.com
class TSMatrix
{public:
//构造函数
TSMatrix( ) {}
//构造函数
//创建一个Mrow行,Mcol列且非零元个数为t的稀疏矩阵
TSMatrix(int Mrow,int Mcol,int t);
//求稀疏矩阵的转置矩阵
void TrMatrix(TSMatrix &);
//快速转置
void FastTrMatrix(TSMatrix &);
//稀疏矩阵相乘
void mulmatrix(TSMatrix &,TSMatrix &);
Triple data[MAXSIZE];//非0三元组表
int mu,nu,tu;//稀疏矩阵的行数、列数和非零元个数
};

#endif // !defined(AFX_XISHU_H__73B83FF2_CCDD_4354_9761_2BEEE23A0B08__INCLUDED_)

类的实现如下
[cpp]
#include "stdafx.h"
#include "xishu.h"

//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////

//创建一个Mrow行,Mcol列且非零元个数为t的稀疏矩阵
TSMatrix::TSMatrix(int Mrow,int Mcol,int t)
{ int m,n,i,j,f0=0;
if(t<=0) exit(0);
ElemType (*A)[MCOL]=new ElemType[MROW][MCOL];
if(!A){cerr<<"内存分配失败!\n";exit(-1);}
for(i=0;i<Mrow;i++)
for(j=0;j<Mcol;j++) A[i][j]=0;
srand(150);
while(f0<=t)
{m=rand()%100;
n=rand()%10;
if(m>=0&&m<Mrow&&n>=0&&n<Mcol)
{A[m][n]=rand()%10;
if(A[m][n]!=0) f0++;
}}
for(i=0;i<Mrow;i++)
{for(j=0;j<Mcol;j++)
cout<<setw(3)<<A[i][j];
cout<<endl;}
}
//求稀疏矩阵的转置矩阵
void TSMatrix::TrMatrix(TSMatrix &T)
{int p,q,col;
T.mu=nu;T.nu=mu;T.tu=tu;
if(T.tu){ //如果T的非0元个数不为0
    q=0;
    for(col=0;col<nu;++col)
        for(p=0;p<tu;++p)
            if(data[p].jj==col){
                T.data[q].ii = data[p].jj;
                T.data[q].jj = data[p].ii;
                T.data[q].e = data[p].e;
                ++q;}}
}
//快速转置
void TSMatrix::FastTrMatrix(TSMatrix &T)
{int col,p,q,t,num[N],cpot[N];
T.mu=nu;T.nu=mu;T.tu=tu;
if(T.tu){
    for(col=0;col<nu;++col) num[col] = 0;
    //先置M每列非0元个数均为0
    for(t=0;t<tu;++t) ++num[data[t].jj];
    //求M中每一列非0元个数
    cpot[0]=0; //M中第一列第一个非元在T中的序号为1
    for(col=1;col<nu;++col)
        cpot[col]=cpot[col-1]+num[col-1];
    //求M中第col列中第一个非0元在T中的序号
    for(p=0;p<tu;++p){
        col=data[p].jj; //记下M中第p个元素的列号
        q=cpot[col];     //该列中第一个非0元在T中的序号
        T.data[q].ii=data[p].jj;
        T.data[q].jj=data[p].ii;
        T.data[q].e=data[p].e;//行、列交换,并赋值
        ++cpot[col];}} //该列下一个非0元序号=上一个序号+1
}
//稀疏矩阵相乘
void TSMatrix:: mulmatrix(TSMatrix &b,TSMatrix &c)
{int i,colB,colA,rowA;
if(nu!=b.mu){
    cerr<<"error\n"; exit(0);}
if(tu*b.tu!=0){
    int *rowSize=new int[b.mu];
    int *rowStart=new int[b.mu+1];
    ElemType *temp=new ElemType[b.nu];
    for(i=0;i<b.mu;i++) rowSize[i]=0;
    for(i=0;i<b.tu;i++) rowSize[b.data[i].ii]++;
    rowStart[0]=0;
    for(i=1;i<=b.mu;i++) rowStart[i]=rowStart[i-1]+rowSize[i-1];
    int current=0,lastInresult=-1;
    while(current<tu)
    {rowA=data[current].ii;
    for(i=0;i<b.nu;i++) temp[i]=0;
    while(current<tu&&data[current].ii==rowA)
    {colA=data[current].jj;
    for(i=rowStart[colA];i<rowStart[colA+1];i++)
    {colB=b.data[i].jj;
    temp[colB]+=d

补充：软件开发 , Vc ,